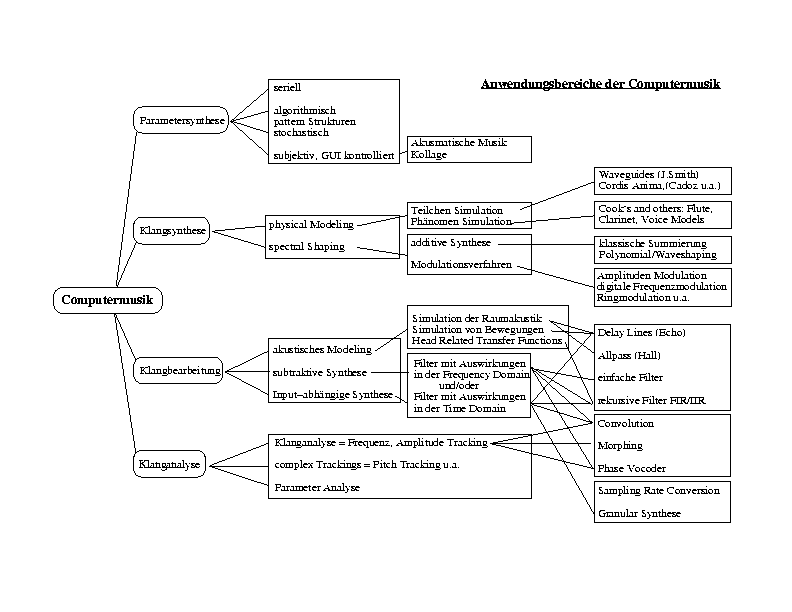

Das wichtigste Kommukationsfenster zu dem Betriebsystem ist die Shell. Das ist ein Fenster innerhalb dessen die meisten Funktionen aufgerufen werden können. Ausserdem existiert noch eine Apple-like graphische Useroberfläche mit Mausclick. Beliebig viele Shells können unter dem Menu Desktop aktiviert werden.
Die wichtigsten Programme, die in dem Kurs benutzt werden sind:
Alle diese Funktionen werden in der Shell aufgerufen. Wichtige Funktionen in der Shell, falls man nicht die Apple-like graphische Useroberfläche benutzen möchte, sind:
Konventionen:
Soundfiles werden mit dem Extension xxx.aiff (SGI) oder xxx.snd (Next) abgespeichert. Soundfiles sollen nicht in den eigenen Folder abgespeichert werden. Dafür stehen die disks /terant-snd oder /exant-snd oder /pikant-snd zur Verfügung. Eine Folderhierarchie wird mit dem "/" (genannt Slash) gekennzeichnet. Der Folder group1 innerhalb des Folders users kann dann mit cd /users/group1/ erreicht werden.
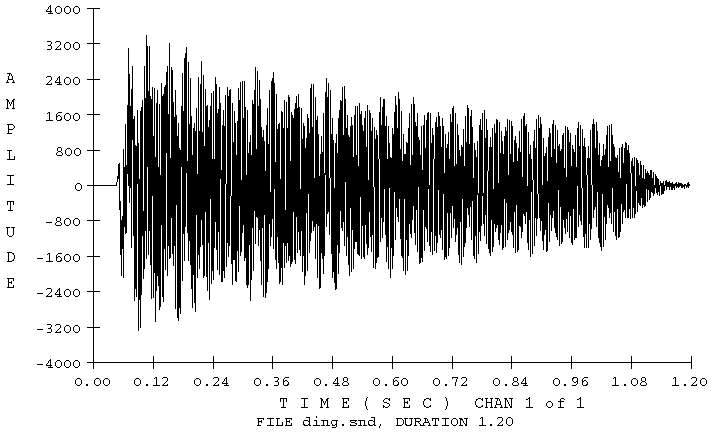
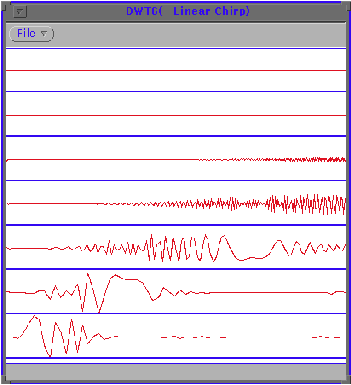
Abb.1 zeigt eine Amplitudendarstellung (die Schwingungen der Luft) eines Gamelan Klanges im Fachjargon Ding genannt
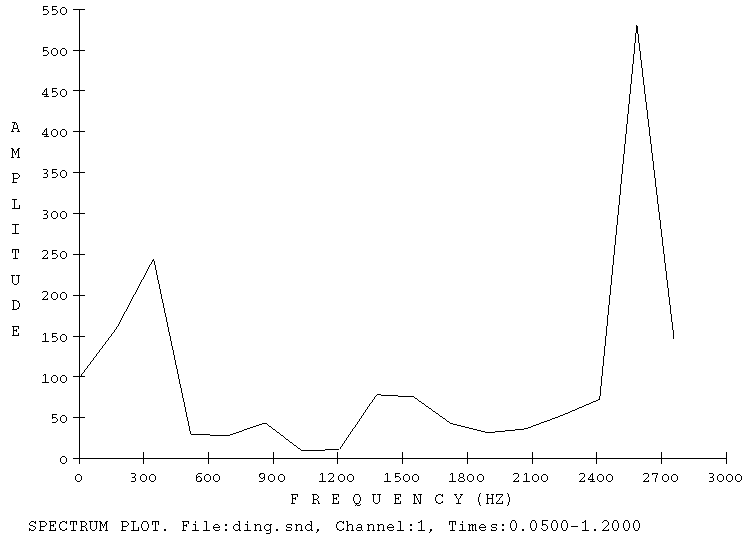
Abb.2 eine klassische FFT in der Frequency
Domain ohne Zeitdarstellung.
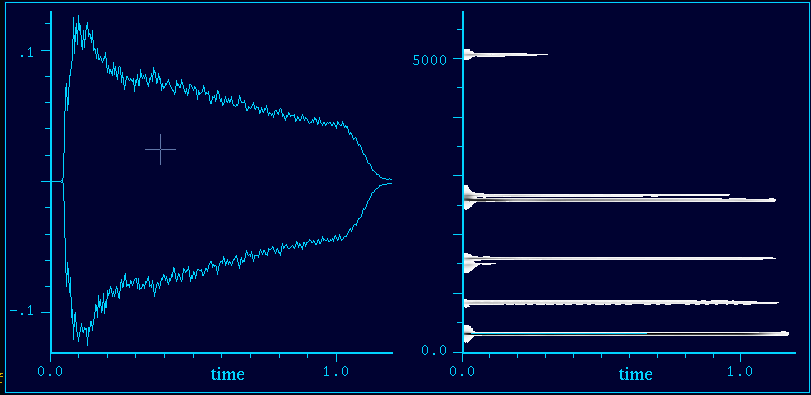
Abb.3 zeigt die Gegenüberstellung einer Amplitudendarstellung und einer DFTdarstellung. Die Frequenzbemessung 1.0 bezieht sich auf die Nyquistrate = Samplingrate * .5, in diesem Fall 22050 Hz.
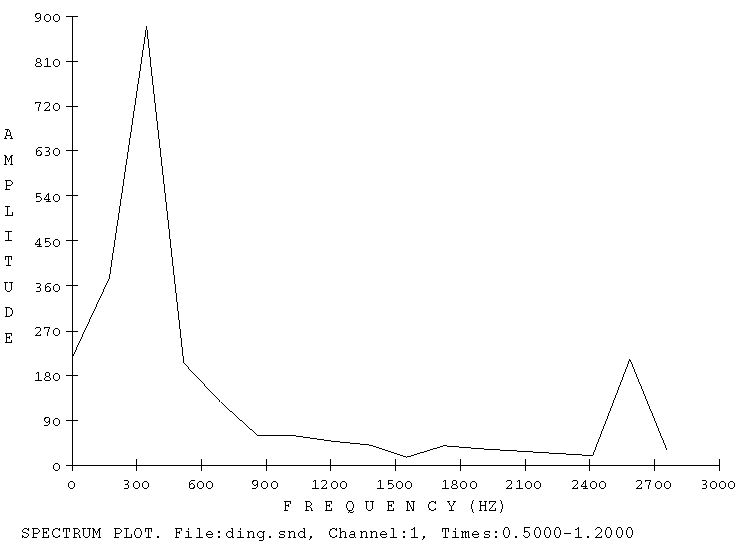
Abb. 4 die FFT der zweiten Hälfte des Klanges.
Hier nun eine Darstellung der Lautstärke der verschiedenen Teiltöne mit einer auf 1.0 normalisierten maximalen Lautsärke.
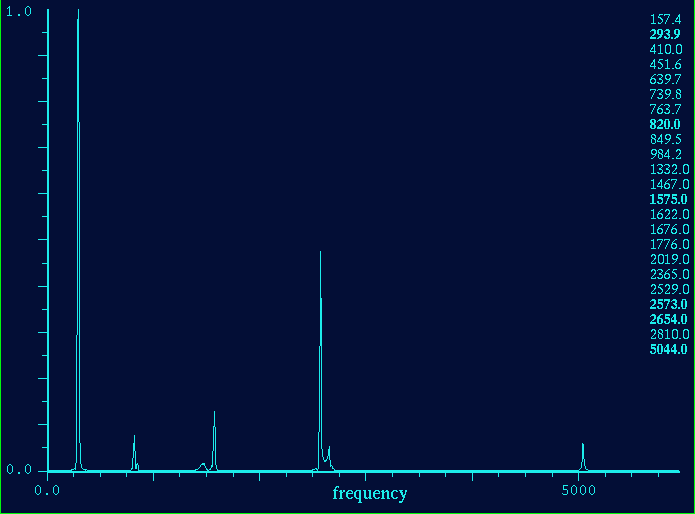
Abb. 5 die FFT des Klanges bei Sekunde 0.85 mit einer differnzierten Analyse der Peakpoints und großem fft-window. Die Zahlen auf der rechten Seite repräsentieren die Frequenzposition von vorhandenen Obertönen. Die bold gedruckten Zahlen stellen die lautesten und damit wichtigsten Obertöne dar.
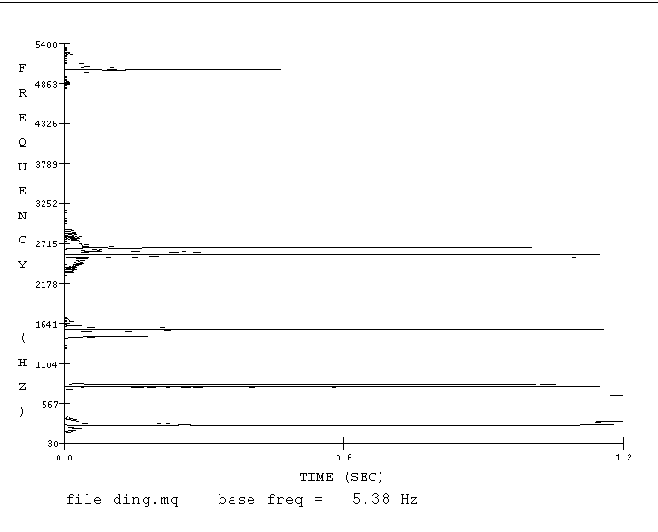
Deutlich sind einige nahe beieinander liegende Teiltöne, sowie
der Grundton bei ca 290 Hz zu erkennen. Wie schon früher in dem Text
angedeutet wurde, vermittelt diese Graphik keinen präzisen Eindruck
von den Lautstärkeverhältnissen des Spektrums. Um diese noch
zu den Informationen der Position der Teiltöne hinzuzufügen,
ist eine 3 dimensionale Graphik nötig, die ähnlich wie das Sonogram
in Abbildung 3 neben Frequenz und Zeit den Lautstärkewert in der 3.
Dimension anzeigt.
Dabei ist die nachstehende Darstellung in gewisser Weise bewertet,
da mithilfe der ermittelten Daten der "Rücken" eines Formanten als
Linie dargestellt wird. Mit anderen Worten wird hier nur der Maximalwert
einer Analysekurve mit einem schwarzen Punkt markiert. Dieser Ansatz ist
durchaus realistisch.Diese Bewertung hilft bei der differenzierten Auswertung
bestimmter Daten, bringt aber auch immer Probleme mit sich.

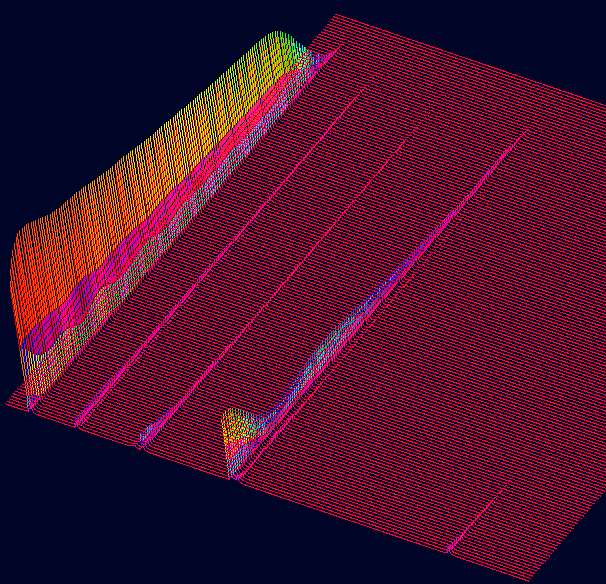
Abb. 7 3-dimensionale Darstellung des Gamelan Tones Ding.
Eine andere Art der 3-dimensionalen Darstellung zeigt ebenfalls die
deutlichsten Formanten. Trotz hoher Auflösung der Analyse lassen sich
jedoch auf den ersten Blick nicht so viele Obertöne ermitteln, wie
in der obigen Darstellung. Die nachstehende Darstellung hat aber einen
mehr körperlichen Charakter also die obige und scheint deswegen räumlich
plausibler. Beide Darstellungen die obige und die nachstehende sind mit
einer grossen Window-size ermittelt. Das erklärt auch die fehlenden
Anfänge der jeweiligen Envelopes: Je größer das erste Analysefenster
ist, desto länger dauert es, bis der erste Wert für den Klang
ermittelt ist. Am besten läßt man für solche Fälle
am Anfang des Klanges ein wenig Platz.
Die Window-size ist für die Qualität der ermittelten Analyse
von erheblicher Bedeutung.
Der Klangalgorithmus bekommt bestimmte Daten denenzufolge er eine Reihe von Zahlen in einen Soundfile auf die Harddisk des Computers speichert. Ein Soundfile ist nichts anderes als eine Datenmenge, die in einer festgelegten Reihenfolge und Geschwindigkeit ausgelesen wird. Die Geschwindigkeit und auch sonstige Daten, wie Anzahl der Kanäle, Länge, Datenformat usw. werden in einem Abschnitt am Anfang des Soundfiles abgespeichert, dem sogenannten Header.
Welche Zahlen schreibt der Klangalgorithmus in den Soundfile hinein?
Das hängt von der Funktion des Algorithmus ab. Falls der Algorithmus einen Klang weiterverarbeiten soll, wird das Programm zuerst eine Zahl aus dem Input Soundfile lesen, diese verarbeiten und dann in den Output Soundfile schreiben. Diese Art mit Klängen umzugehen nennt man naheliegenderweise Klangverarbeitung und entspringt der Musique Concrete, die mit existierenden Klängen umgeht. Wird ein Klang vollständig künstlich erzeugt, so spricht man von einer Klangsynthese. Ein Sinustongenerator ist ein solcher Synthesegenerator. Diese Technik wurde auch im WDR Studio in Köln entwickelt und von Eimert Koenig und Stockhausen exessiv bentutzt (Kontakte).
sinus ( 1Kreis * Gesammtanzahl der Kreise * Zeitposition + Anfangsposition)
sin(2pi*f*t+phi)
Die Position des Zeigers kann nun auf 2 Arten beschrieben werden:
Wird dieser Text in einem File z.B. mit dem Namen test.ins abgespeichert. So braucht er nur mit
:cl /terant-snd/test.ins
compiliert und geladen werden, bevor er mit dem Ausdruck
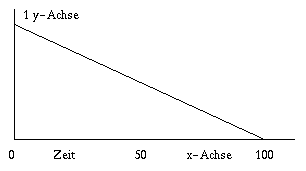
Abb. 9 Breakpoint-Kurve '(0 1 100 0)
Eine solche Interpolation besteht also, wie wir gesehen haben aus 2 Werten:
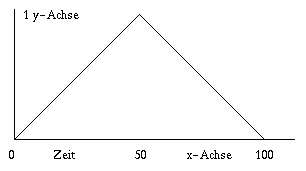
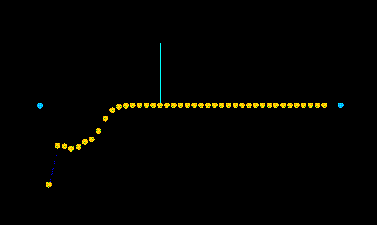
Soll die Envelope bei 0 beginnen, um in der Mitte nach 1 zu steigen und später wieder zu sinken sähen die Daten und der Envelope verlauf wie in Abbildung 7 dargestellt aus.
Wird die Lautstärke eines Generators mit einem anderen Generator angesteuert, so entsteht ein Spektrum, das den Ton des angesteuerten Generators fc (frequenc des Carriers, Trägers) in originaler Lautstärke enthält. Von Amplitudenmodulation spricht man jedoch nur, wenn eine Konstante zu dem Modulationssignal addiert wird, die zur Folge hat, daß das Trägersignal in einer mindestlautstärke immer präsent ist. Zusätzlich besteht das Spektrum aus einem Teilton mit der Frequenz fc + fm und einem dritten Teilton mit der Frequenz fc - fm die jeweil mit halber Lautstärke erklingen.
Verglichen mit der spezifischen Leistungsfähigkeit der alten Maschinen, ist die neue Hardware zwar hunderte mal schneller, als die alten Mainframes (Supercomputer), jedoch ist die Leistungsfähigkeit Summa summarum nicht besonders gestiegen. Die langsamen Computer wurden mit einer hochoptimierten teueren Spezialhardware wettgemacht - die Samson Box konnte nur Samples synthetisieren und war nicht frei programmierbar wie ein Computer, der alles mögliche rechnen kann. -- Aber das nur am Rande.
Dieses Verfahren Generatoren miteinander zu modulieren kannte man schon lange aus der Rundfunktechnik. Bei dem Radiosignal wird ein Audiosignal auf eine sehr hochfrequente Schwingung aufmoduliert. Das gleiche Verfahren wird bei einem Tonbandgerät angewandt, um eine bessere Klangqualität zu erreichen. Chownings Leistung bestand nun darin die Theorie für die Anwendung als musikalisches Instrument zusammenzutragen und zu ergänzen und vor allem darin, die modifizierte Theorie der digitalen Frequenz Modulation zum ersten male zu verwirklichen.
Die Frequenz Modulation besitzt den Vorteil, das mithilfe weniger Generatoren Klänge mit reichhaltigen Spektren nicht nur erzeugt werden können, sondern auch in der präzisen Kontrollmöglichkeit, die dieses Verfahren bietet, sodaß gezielt bestimmte Spektren erzeugt werden könnnen.
Das Resultat einer FM läßt sich folgendermassen beschreiben:
Die Modulation eines Generators mit der Frequenz fc
durch einen Generator mit der Frequenz fm, der mit der
Amplitude k multipliziert wird, ergibt neben dem zentralen Ton fc
folgende
Teiltöne:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Die Liste läßt sich beliebig weiterführen, da der Wert für k beliebige Größen haben kann. Auf der linken Seite der Liste, wo eine Subtraktion zwischen Carrier und Modulator stattfindet, befinden sich die Teiltöne die unterhalb der Carrier Frequenz liegen und auf der rechten, die Teiltöne, die oberhalb des Carriers liegen. Auffällig ist die Tatsache, daß jeder für k ungradzahlige Teilton unterhalb des Carriers eine negative Amplitude erhält. Das hat mit der Phase mit der dieser Teilton schwingt zu tun und ist von Bedeutung, falls die Frequenz eines Teiltones in den negativen Raum fällt. Ist dieses der Fall, so wird der Wert dieses Tones um den O-Punkt wieder zurück in den positiven Bereich geklappt und in dem Amplitudenwert mit -1 multipliziert. Fällt dieser geklappte Teilton wieder zurück auf einen vorhandenen Teiton, so werden diese beiden Töne in der Amplitude addiert. Das folgende Beispiel soll den ganzen Vorgang beschreiben.
In der Abbildung 8 befindet sich unterhalb des Plots die mathematische Beschreibung der FM: 2pi entspricht einer Periode, 400 ist die Anzahl der Perioden und t die Zeiteinheit in der diese Perioden schwingen. In der großen Klammer befindet sich noch eine kleinere Klammer, die den Modulator beschreibt, der 2pi * 400 * t = 400 Hz schnell schwingt und den Modulationsindex, also die Lautstärke des Modulators von 1 besitzt.
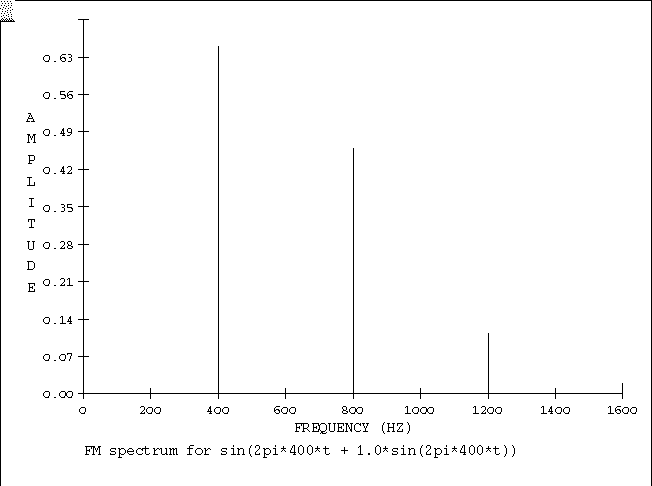
Abb. 11 zeigt das Spektrum einer FM mit fc = 400 fm=400 und k=1
Ein solches FM Spektrum kann sehr einfach mithilfe der Funktion fmplot in einer Shell dargestellt werden. Dazu fmplot in die Shell schreiben und danach die Taste "Enter" drücken. Daraufhin fragt das Programm:
Give <Carrier-Freq> <Modulation-Freq> <Index>:
versucht es mit: 400 400 1 und Ihr werdet die obige Abbildung erkennen können.
Wichtig beim spektral modelling mit FM ist die Lautstärke der einzelnen Teiltöne. Es genügt ja nicht, daß bestimmte Teiltöne vorhanden sind, sie müssen auch in einem bestimmten Lautstärkeverhätlnis zueinander stehen. Diese Amplituden lassen sich mithilfe einer mathematischen Funktion, der Bessel Funktion ermitteln. Diese kann in dem Lisp Fenster mit der Funktion bessel-jn abgerufen werden. Wird die Seitenbandnummer und der Index angegeben, so gibt dieser Ausdruck die relative Lautstärke des angegebenen Seitenbands aus.
bessel.lisp darin: (bes-jn <Sidebandnummer> <Index>)
Bei der Auswertung der Bessel Funktion läßt sich erkennen, daß eine Art Verteilung der Energie stattfindet: Hat das Spektrum nur wenig Teiltöne, wie z.B. bei k=0, wo nur der Carrier erklingt, so haben diese Teiltöne eine hohe Lautstärke. Je mehr Teiltöne erklingen, als bei hohen k Werten, desto leiser sind diese Töne.
Rechnet man nun das obige Beispiel durch, so entstehen folgende Frequenzen.
fc=400 fm=400 k=1
Das Spektrum besteht aus: fc, fc-fm, fc+fm. Das sind die Hauptteiltöne, die in der Anzahl ungefähr nach der Regel k * 2 + 1 ermittelt werden können. Das bedeutet in diesem Falle 3 circa Teiltöne. Es entstehen immer mehr Teiltöne, die jedoch in ihrer Lautstärke so stark vom übrigen Spektrum abfallen, daß sie keine große Bedeutung mehr für den Eindruck des Gesamtsprektrums hinterlassen. Das Ergebnis heisst also: 400 Hz, 0 Hz, 800 Hz. Man kann dieses Ergebnis deutlich an dem Spektrum ablesen. Falls k=2 wäre, so würden ca. 5 siginifikante Teiltöne entstehen: fc, fc-fm, fc+fm, fc-2fm, fc+2fm= 400, 0, -400, 800, 1200. Die Frequenz -400 Hz würde um den 0 Punkt gespiegelt + 400 Hz ergeben und, in der Amplitude als negativer Wert zu fc=400 addiert, mit anderen Worten also subtrahiert. Alle sonstigen negative Spektren werden nach diesem Additionsvorgang als positive betrachtet. Der negative Werte spielt nur bei der Addition der Schwingungen eine Rolle - ist ja auch logisch, denn eine phasenverschobene Schwingung wird von unseren Ohren genause wahrgenommen, wie eine nicht phasenverschobene Schwingung, während die Addition zweier gleichfrequenter gleichlauter Schwingungen, von denen eine Phasenverschoben ist, zu einer Auslöschung der Schwingung führt. Genau um diese physikalische Tatsache geht es hier. Dieser Vorgang hat zu Folge, daß das Spektrum bei k=2 einen deutlich leiseren Grundton von 400 Hz hat, während der 800 Hz Ton, bedingt durch den Wert der Bessel Funktion deutlich lauter ist.
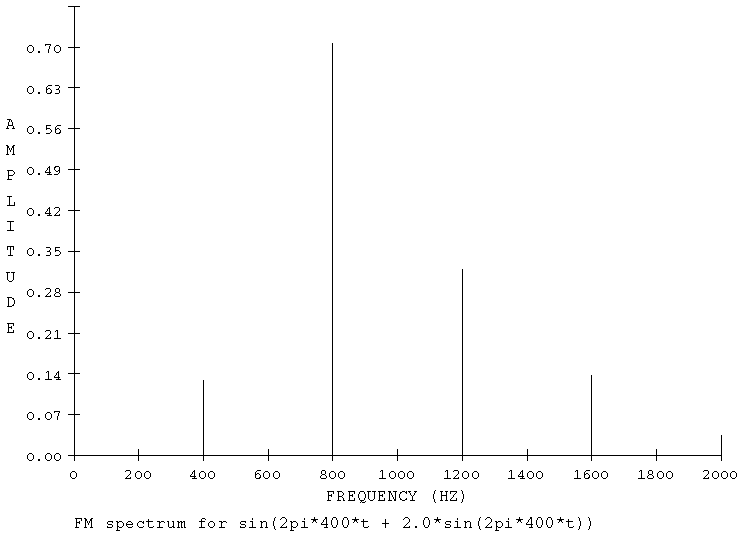
Abb. 12 Spektrum Plot der FM von fc=400 fm=400 k=2.
Für die Einschätzung des resultierenden Spektrums ist das Frequenzverhältnis zwischen dem Carrier und dem Modulator verantwortlich. Die sogenannte Carrier-Modulator Ratio gibt einen Hinweis auf die Konsistenz der resultierenden Spektrums:
Bei fc=400 fm=400 ist die Ratio 1/1.
fc/fm=N1/N2
fo=fc/N1=fm/N1 wobei fo den Grundton darstellt
für N2=1 enthält das Spektrum alle harmonischen, also zum Grundton ganzahligen Teiltöne
für N2=M, wobei M eine ganze natürliche Zahl darstellt, fehlt in dem Spektum fo jeder Mte Teilton.
für N2=1 oder N2=2 fallen die resultierenden negativen Teiltöne nach der Klappung um Null (das entspricht der Ermittelung des absoluten Werten, bzw. der Umwandlung des negativen Vorzeichens in ein positives) mit entsprechenden positiven Teiltönen zusammen und müssen mit diesen addiert werden.
In unserem Beispiel oben ist die Ratio 1/1, fo ist 400/1, der Grundton ist also 400 Hertz, wobei N2=1 anzeigt, daß jeder Oberton des 400 Hz Grundton in dem Spektrum vorhanden ist.
John Chowning ermittelte in langer Forschungsarbeit equivalenzen zu existierenden instrumentalen Spektren. Die Grundlage dieser Spektren lassen sich mit einer einfachen FM realisieren und fussen auf folgenden Angaben:
Dazu eine noch eine Abbildung, die den Hauptausschnitt des Klange ein wenig differenzierter zeigt.
In den Abb. 6-8 ist das Spektrum des Gamelan Tones präziser dargestellt.
Deutlich sind einige nahe beieinander liegende Teiltöne, sowie der
Grundton bei ca 290 Hz zu erkennen. Wie schon früher in dem Text angedeutet
wurde, vermittelt diese Graphik keinen präzisen Eindruck von den Lautstärkeverhältnissen
des Spektrums. Um diese noch zu den Informationen der Position der Teiltöne
hinzuzufügen, ist eine 3 dimensionale Graphik nötig, die ähnlich
wie das Sonogram in Abbildung 3 neben Frequenz und Zeit den Lautstärkewert
in der 3. Dimension anzeigt.
Dabei ist die Darstellung 7 in gewisser Weise bewertet, da mithilfe
der ermittelten Daten der "Rücken" eines Formanten als Linie dargestellt
wird. Mit anderen Worten wird hier nur der Maximalwert einer Analysekurve
mit einem schwarzen Punkt markiert. Dieser Ansatz ist durchaus realistisch.Diese
Bewertung hilft bei der differenzierten Auswertung bestimmter Daten, bringt
aber auch immer Probleme mit sich.
Eine andere Art der 3-dimensionalen Darstellung(Abb. 8) zeigt ebenfalls die deutlichsten Formanten. Trotz hoher Auflösung der Analyse lassen sich jedoch auf den ersten Blick nicht so viele Obertöne ermitteln, wie in der obigen Darstellung. Die nachstehende Darstellung hat aber einen mehr körperlichen Charakter also die obige und scheint deswegen räumlich plausibler. Beide Darstellungen die obige und die nachstehende sind mit einer grossen Window-size ermittelt.
Falls die Ratio der Modulatoren für die Resynthese diese Klanges nun klar ist, hilft ein Detail aus dem Spektrum, um zu verstehen, was hier im Einschwingvorgang des Klanges vor sich geht.
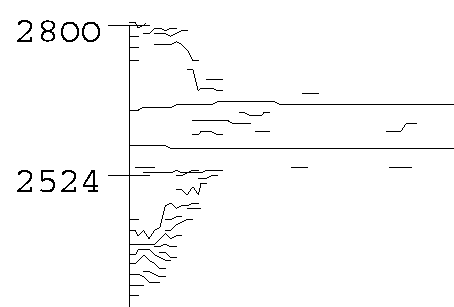
Abb. 13 Detail aus dem Einschwingvorgang des Gamelan Tones.
Es sind am Angang des Klanges viele kleine einzelne Teiltöne vorhanden, die dicht beieinander liegend die Hauptfrequenzen umlagern. Außerdem bleiben diese Teiltöne nicht durchweg gleich. Sie verändern ihre Freuquenz glissandoartig. Selbst die Hauptfrequenzen bleiben am Anfang nicht statisch und bewegen sich auf und ab.
Sinnvoll war auch die Integration von Rauschgeneratoren, um im komplexen Vorgang des Einschwingens von Instrumenten den hohen Geräuschanteil zu integrieren, oder die Kombination mit Filtern, die eine konstante Formantstruktur ermöglichten.
4.6.3.3 Praktische Beispiele und Übungen von Nicky Hind
Frequency Modaulation Tutorial Part1 und Part 2
Im allgemeinen hat sich der Begriff des Waveshaping nur in bestimmten Zusammenhängen etabliert, das das Verfahren, das Abbilden der Amplitudenbewegungen eines Signales die Veränderung von Zeit, wie sie jeder Filter durchführt (phasenverschiebung), nicht direkt impliziert. Der Waveshaper verändert bildet eine Sampleposition mithilfe der transfer function auf eine neue ab.
yn=xn + a * x n-1
wobei n die Sample Nummer darstellt und a die Lautstärke in der das verzögerte Signal hinzugemischt wird.
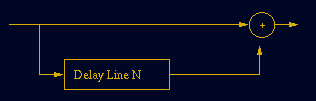
Hier ein paar andere Beispiele einer Gleichung:
one-zero filter: y(n) = a0 x(n) + a1 x(n-1)
two-zero filter: y(n) = a0 x(n) + a1 x(n-1) + a2 x(n-2)
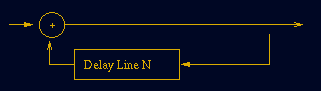
Hier ein paar Beispiele für Filter mit Recursiven Elementen. Man erkennt sie ganz leicht an dem y auf der rechten Seite der Gleichung:
one-pole Filter: y(n) = a0 x(n) - b1 y(n-1)
two-pole Filter: y(n) = a0 x(n) - b1 y(n-1) - b2 y(n-2)
Um einen Equalizer Filter zu benutzen schreibe gQ in eine Shell.
5.4. Convolution von Signalen
Bei der Convolution von Signalen werden die Samples zweier Signale alle miteinander multipliziert. Da das aber eine ziemlich aufwendige Arbeit ist, gibt es Formeln mithilfe derer die Convolution überhaupt durchführbar ist.
Die Convolution zwischen zwei Signalen hat Auswirkungen auf die Frequenz und die zeitliche Anordnung des Signales. Eine optimale Form der Verhallung ist die Convolution des Signales mit einer Impuls-Antwort eines Raumes.
Die urspruengliche Form bestand aus einem in den 30er Jahren von Homer Dudley entwickelten Channel Vocoder. Der Vocoder entstand aus der Idee ein Signal, vornehmlich das Stimmensignal, in verschiedene Kanaele zu zerlegen und die einzelnen Kanaele auf ihre Notwendigkeit hin zu überprüfen. War kein Signal in einem Kanal vorhanden, so konnte dieser weggelassen werden ohne das Signal zu beschaedigen. Der Zweck der Forschung bestand in der Aufgabenstellung, mehrere Signale gleichzeitig durch ein und dasselbe Kabel zu senden. Da die Informationsdichte innerhalb eines Kanales weniger hoch ist, als die Informationsdichte des Gesamtsignales, war es wahrscheinlich, dass weniger Information zur Uebertragung des Signales notwendig war. Mit anderen Worten entsprach dieses dem Versuch das Signal zu komprimieren.
Phase Vocoder funktioieren allgemein gesagt wie eine Filterbank, die
mit einer Oscilatorbank gekoppelt ist. Dabei ermittlet die Filterbank Daten
bezueglich der Frequenz. Dieser wird durch den Filterbereich des Filters
ermittelt. Ausserdem ermittelt der Filter einen Amplitudenverlauf dieses
Teiles des Spektrums.
Die unten stehende Graphik verdeutlicht die Funktion eines Phasen Vocoders.
In der Analyse wird eine FFT durchgeführt, die die einzelnen Teiltöne
und der Lautstärken ermittelt. Diese Daten werden sowohl zur graphischen
Darstellung eines Klanges benutzt, als auch zur Resynthese. In der Resynthese
wird für jeden, in der FFT befindlichen Punkt, der eine Lautstärke
über 0 besitzt ein Osciliator angesteuert, der an dieser Stelle einen
Ton in gewünschter Tonhöhe und Lautstärke erzeugt. Nimmt
man z.B. die gelbe Scheibe in der unteren Darstellung, die den Grundton
auf einer Frequenuz von 291 Hz darstellt, so würde hier der Oscilator
einen Sinuston mit der in der gelben Scheibe dargestellten Lautstärkekurve
erzeugen.
Da die Töne aber wie bei einem Vibrato nicht immer genau auf einer
Frequenzposition bleiben, wird ein Oberton mit einer gewissen Vibrato Breite
ausgestattet. Der 1. Teilton bleibt als 1. Teilton bewertet, obwohl er
ein paar Hertz auf und ab glissandiert. Erst wenn sich der Ton zu sehr
von seinem Zentrum entfernt, würde er als neuer Teilton mit neuer
Amplitudekurve bewertet.
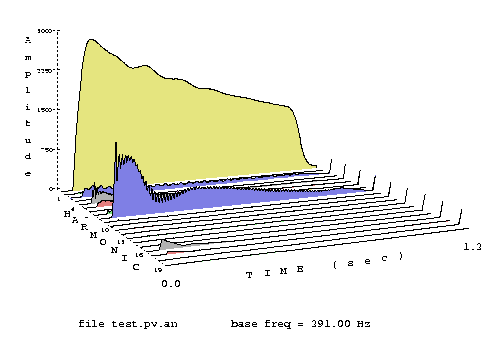
Abb. 13 Spektrum des Klanges Ding mit farbiger Scheibendarstellung.
7. Granulare Synthese
7.1. Funktionsweise
Eine Einführung zum Einlesen und modifizieren von Samples findet sich in Nicky Hinds Signal Processing Manual.
Parallel zur elektronischen Musik, entwickelte sich der Strang der Signalverarbeitung
und der der Samplebearbeitung. Die Signalverarbeitung verändert ein
existierendes Signal. Filter und Phase Vocoder gehören zu dieser Gruppe.
Die Samplebearbeitung manipuliert die Samples an sich. Das heißt,
daß die Reihenfolge der Samples in irgendeiner Art und Weise verändert
wird. Die Funktionalität dieses Prozeßes läßt sich
durchaus mit der der DFT vergleichen. Ein Fenster mit einer konstanten
oder variable Größe geht das Sample entlang um jeweils einen
bestimmten Abschnitt aus dem Sample auszulesen. Die ausgelesenen Abschnitte
werden in dem neu zu erstellenden Sample wieder in einer neuen Anordnung
zusammengefügt.
Die Hop-Size bestimmt nun wie groß der Abstand zwischen jeweiligen
Auslesepositionen des Fensters ist, wie weit also die Ausleseposition weiter
"hüpft". Aus der Fenstergröße und der Hop-Size ergibt sich,
inwieweit Teile des Samples doppelt ausgelesen werden.
Für das Resultat der "Dekomposition" eines Samples ergeben sich
demnach zwei wichtige Aspekte:
1. Wie ist die Leseanordnung strukturiert.
2. Wie ist die Schreibanordnung strukturiert.
Beide Strukturen determinieren den sich ergebenden Klang. Es ist garnicht
so einfach, durch bloße Vorstellungskraft zu ermitteln, welche Resultate
kompliziertere Lese- und Schreibestrukturen zur Folge haben.
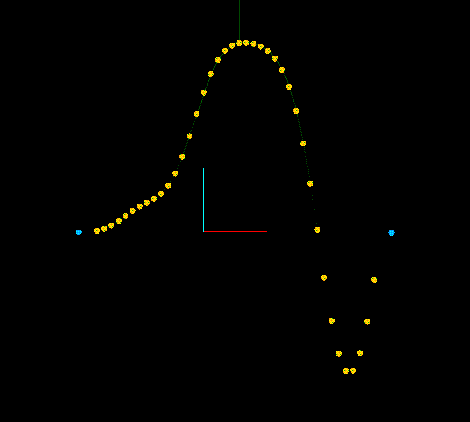
In dem unteren Bild sind verschiedene Möglichkeiten gezeigt, einen
immer gleichen Sampleblock in einen Soundfile zu schreiben.
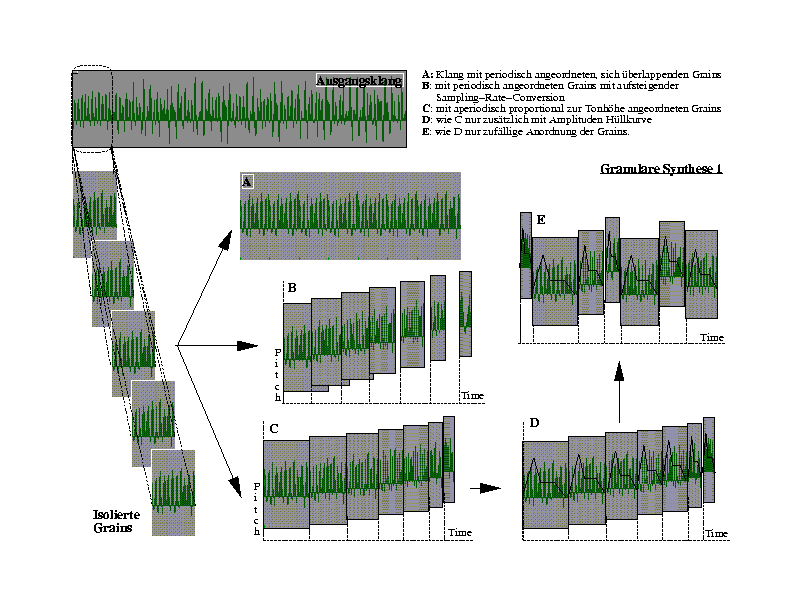
7.2. Spektrale Konsequenzen der Granularsynthese
Die Dekomposition einer Schwingung hat natürlich Konsequenzen für
die resultierenden Spektra. Woher kommen diese Veränderungen und wie
lassen sie sich kausal auf die Dekompositon zurückführen?
Um dieses Phänomen zu verstehen lassen sich am besten Sinustöne
benutzen. Wird ein Sample mit Sinustönen in Grains zerteilt, so entstehen
bei der Zusammenfügung der Grains scharfe Kanten im Schwingungsverlauf.
Dieses geschieht in direkter Abhängigkeit von der Window Größe.
Entspricht die Window Größe der Länger einer oder mehrerer
Periodendauern einer Schwinung, so ergibt sich bei dem Zusammenfügen
der Abschnitte ein "glatter" Schwingungsverlauf. Man kann in diesem Fall
fast von einem Resonanzverhalten des Windows sprechen. Anders als bei einer
normale Resonanz werden die im Verhätlnis zur Größe des
Resonators ganzzahligen Schwingungen nicht verstärkt, sondern bleiben
gleichlaut. Ebenfalls andersal bei einem normalen physikalischen Resonator
werden Schwingungen zu ursprünglichen Signal hinzugefügt: Die
Schwingungen, die bei den Kanten und Ecken entstehen. Das würde zweifelsohne
ziemlich hochfrequente dominante, mit anderen Worten störende Klänge
ergeben. Um dieses negative Phänomen in den Griff zu bekommen arbeiten
die meisten Granulierungs Prozeduren mit Envelopes, die die Lautstärke
am Anfang eines Gains langsam Anheben und ebenso langsam wieder absenken.
Die Form dieses Fensters kann bei kurzen Graindauern ebenfalls die Obertonstruktur
bestimmen und wie eine Art Generator wirken. Deshalb ist diese Window-Type
von entscheidender Bedeutung. Solche Fenster sollten abrubte Schwingungsveränderungen
möglichst vermeiden. Deshalb bieten sich sinusähnlich Fenster
an. Gebräuchliche Fenster sind Hämming, Hanning, Welch usw. und
sind auch in der DFT gebräuchlich.
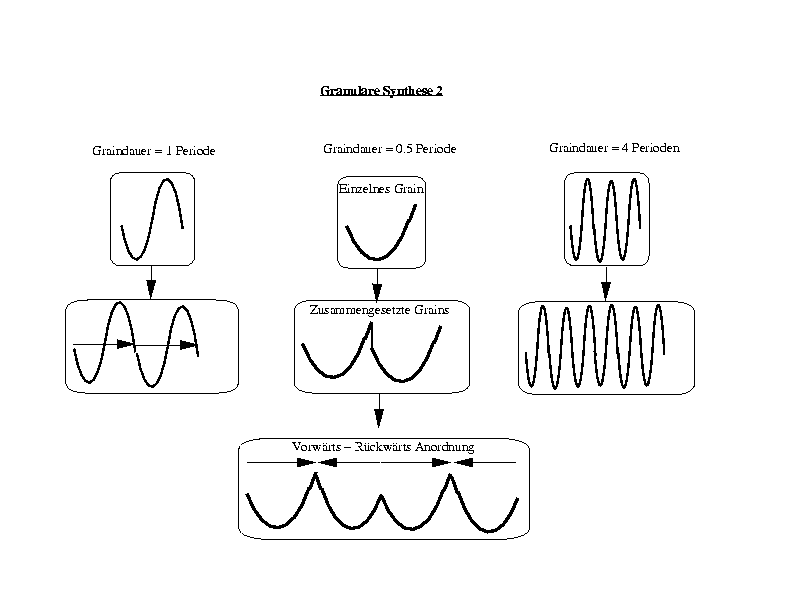
7.3. Psychoakustische Konsequenzen granulierter Klangpartikel
7.4. Fraktale Strukturen
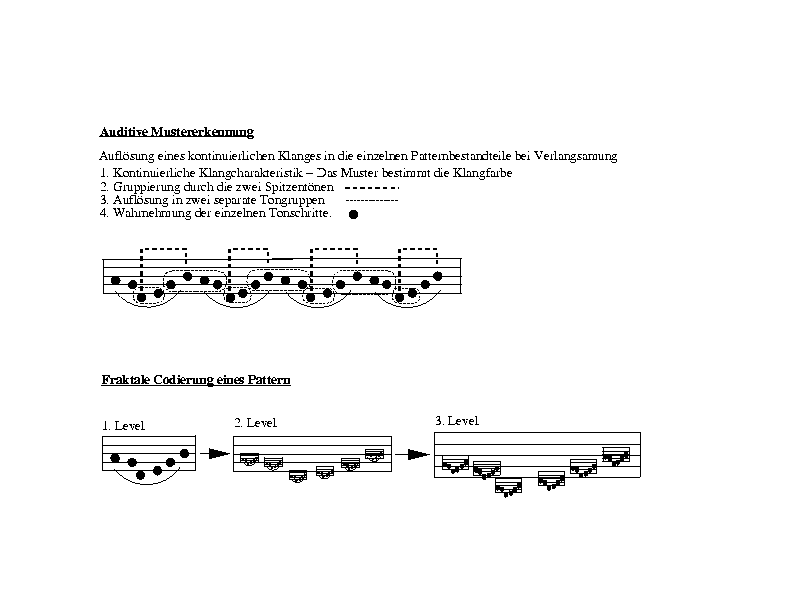
7.5. Strukturmodelle
Die Tonhoehen der Transposition ab 14'40'' entsprechen den Toenen b6 d6 d5 fs4 b3 f3 a2 e2, wobei a4=440Hz. Das entspricht in Bezug auf das Sample und dessen urspruenglicher Tonhoehe einer Transpositionsreihe von: 7.56 4.49 2.24 1.41 0.94 0.67 0.42
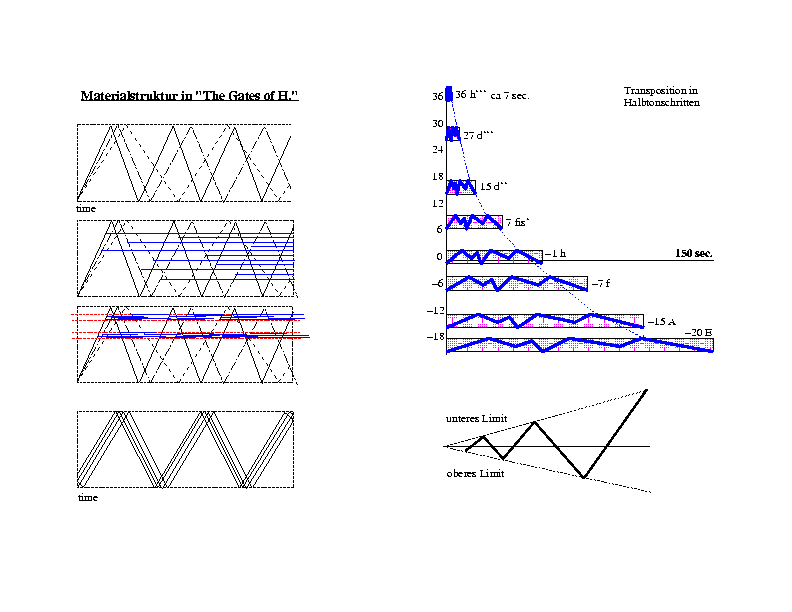
7.6 Beschreibung des Programmes "Granular" von Gerhard Behles
granular 0.30 manual ________________________________________________________________________________
Introduction ____________
granular 0.30 is a real-time audio processing software running on Silicon Graphics Indigo / Indy workstations.
The purpose of the program is to provide a tool for altering sound morphologies.
Any sound can be used for modification by the program. Modifications can range from subtle to drastical, depending on parameter settings.
granular 0.30 modifies sounds by de-composing them into small chops, so called grains, and by re-assembling those grains in some manner.
This work has departed from the granular synthesis technique that has been developed by Barry Truax. For understanding granular0.30, let's start with classical granular synthesis:
An overview over the granular synthesis technique _________________________________________________
the result of granular synthesis is a stream of so called grains. a grain is a piece of sound with a duration between 2 milliseconds and several hundrets of milliseconds (5 ms is a typical mean value); no matter what the under- lying sound material is, the grain has an envelope shape with some degree of fade-in- and fade-out time. these attack- and release-portions of the envelope make sure that no truncation noises (clicks) will be heared, regardless of transients in the material. the choice of material to use for granular synthesis is basically independent of the model: sinewaves, fm-sound and concrete sound (sound samples) or whatever. in order to achieve continous sound output, grains are fired repeatedly. truax' model organizes grains in VOICES. one voice plays a grain, is silent for a while, plays a grain again, is silent again etc. this process can be controlled using two paramters: the grains DURATION and the DISTANCE between grains. the sum of the values for duration and distance is the PERIOD of a grain cycle. since typical values for distance and period lie in the milli- second range, a sensation of pitch will arise from the grain cycle, overlaying and interfering with the underlying material's pitch (if the material is pitched, that is). In fact, this process can be regarded as a form of AMPLITUDE MODULATION, and the sound that is obtained with short periods is often being associated with ring modulation. a source of statistical deviation is being introduced to inrich the quality of the synthesized sound: each time a grain is fired, a couple of random operations are invoked in order to determine this grains duration, its distance from the following grains, and maybe other parameters that influence what the grain sounds like; for example the PITCH or TRANSPOSITON of the underlying material. In fact, each of the relevant parameters, ie duration, distance, pitch, etc. is accessed by a pair of values: one FIX value and one RANGE value, where the result of a random operation is the "fix" value plus a random number between zero and the "range" value. so with a duration fix value of 10 ms and a duration range value of 5 ms you would be getting grains of a duration between 10 and 15 ms, or 12.5 ms average; with a steady, unbiased value for distance of, say, 20 ms this would result in a period varying between 30 and 35 ms, or in a grain FREQUENCY fluctuating between 33.3 Hz and 28.5 Hz. grain frequency in one voice is equivalent to the so called GRAINS PER SECOND value. at high grain frequencies, the effect of increasing duration and distance range values is often associated with adding NOISE. grain density is enriched by increasing the number of voices. each voice is doing the same thing (the process that has been described above) and is being controlled by the same set of paramters. so there is only one knob for grain duration fix no matter how many voices are sounding. in fact, as long as all range values remain zero, all voices will sound equal and in phase, so they will just sound like one voice at a higher amplitude. as the range value for, say, duration is increased, the onset of grains will be smeared among the voices, and the voices will be completely out of sync at some point. this is because new random deviations are being calculated with each grain's onset, and the grains in the different voices will be drifting apart as a consequence.
modifications of the granular technique _______________________________________
The technique that has been described above has been modified and extended in a veriety of ways.
First, grains in one voice can overlap; a grain distance value around zero results in an overlap of four grains in each voice. In this manner, sound can be continouus in one voice, since no "holes" or "breakes" are heared.
Apart from using random deviation, a spreading of values among voices can be applied for a couple of parameter groups. The "spreading" value will equally distributed among the voices and then be added to the fix value. Using four voices, a spreading value of four will result in 1 being added to the fix value for the first voice, two for the second etc. A spreading value of ten will add two to the first voice, four to the second etc.
Grains are made from excerpts of the input sound. By picking excerpts in the order and distance that corresponds to the input sound, the input sound can be "re-assembled". By alterning speed and direction of the input sound's traversal, sound can be slowed up or down arbitrarily. The choice of input sound excerpts can also be randomized.
The amplitude level of the input signal excerpt that a grain is made of can be measured and used to bias the program's behaviour in variety of ways.
real time _________
Because the program is running in real time, there is some restriction concer- ning the complexity of operations. If the computer is overpowered by what it is told to do, it will start producing "wholes" in the audio output. This will do no harm to the computer, but it will sound disturbing. When changing parameters, you are varying the computation load; it is rather easy to learn "how far one can go" in the limits of one's machine, when using the "gr_osview" program, that comes with SGI computers. This program gives a graphic overview over system load. Run it in the background of granular0.30 and see how much green space (idle time) is left depending on what you do.
Mind that the system sampling rate affects the amount of computation that can be done. You can set the system sampling rate before calling granular0.30 (the system samplerate needn't match the samplerate of the soundfile you are processing).
how to start the program ________________________
the program is called "granular" and is launched from a SHELL window by typing the word granular followed by the name of an AIFF-formatted MONO audiofile. use "soundfiler" to convert other formats (eg AIFC) to AIFF, or stereo to mono. the audiofile's samplerate needn't match the system's output rate, the program will convert the samplerate in realtime. the audiofile must be located in the working directory, meaning in the directory that you launched the program from, or in a directory that can be set in a system variable called SFDIR. as the program comes up, the soundfile is heared unaltered and played back in a loop. That doesn't mean that the process of granulation has to be initiated; in fact the program is always granulating. In the default setting, succeding grains will overlap and pick excerpts of the soundfile in a way that perfectly reconstructs the original.
overview over program controls ______________________________
1. buttons
- 0 - 31 (numbered buttons on the right) clicking on those buttons will recall any presets stored under this number. A preset is like a snapshot of the faders. clicking on a preset button while holding the LEFT shift-key will strore the current fader position at that preset location. Any preset-button that stores a preset has a sign around the number (" > < "). - quit termintates the program. If SGI's standard MIDI-server is running, this might crash your computer. Terminate by double-clicking in the left square of the top window frame. - load after clicking on "load", you can type the file-name of a preset file into the shell that you launched the program from. The preset file contains 32 preset settings to be recalled by clicking on one of the buttons numbered 0 - 31. The preset file must be located in the current working direc- tory. - save after clicking on "save", you can type any file-name, under which the state of the current 32 preset locations will be stored. - reset synchronizes all voices.
2. continuous parameters (as they appear on the window, left to right)
PARAMETER GROUP Soundfile Position __________________
INTRODUCTION Grains are modifications of excerpts from the input soundfile; these parameters help to specify which excerpt is to be taken for each grain. There is a global index into the input soundfile; each grain is made from an excerpt at or around that index. The index is advancing with some direction and speed, and it is constrained to a range in which it is cycling in the manner of a loop. The soundfile excerpt that a grain is taken from is chosen according to the current position of the soundfile index plus (possibly) some random deviation and some spreading among voices.
ABBREVIATION pos PARAMETER Soundfile loop startpoint DESCRIPTION Startpoint of the soundfile index loop. UNITS / SCALE linear scale 0 to 1. corresponds to the entire soundfile duration (0.5 = middle of the soundfile). this fader's position relates to the soundfile overview on the left.
ABBREVIATION dev PARAMETER Soundfile loop length DESCRIPTION Length of the soundfile index loop. UNITS / SCALE linear scale 0 to 1. corresponds to the entire soundfile duration (0.5 = middle of the soundfile).
ABBREVIATION spd PARAMETER Soundfile traversal speed fix value DESCRIPTION This is the speed of soundfile index advance. A value of 1 indicates that the index is advancing with the same speed as the original soundfile; -1 is the original speed, but reverse direction. 0 is no advance, i.e. a freeze of motion. UNITS / SCALE linear factor ranging from -2 to 2. negative values indicate reversed direction.
ABBREVIATION stRG PARAMETER Soundfile position random deviation range DESCRIPTION Range of a random noise source that will add some deviation to the choice of excerpts. UNITS / SCALE linear scale 0 to 1. corresponds to the entire soundfile duration (0.5 = middle of the soundfile). The selected value is the maximum value that the random number source can produce.
ABBREVIATION stSP PARAMETER Soundfile position spreading factor DESCRIPTION Normally, grains in all voices are made from excerpts according to the current soundfile index. This parameter serves to spread this value among voices; in each voice, the index will be offset by equal portions of the value given, introducing some delay between voices. UNITS / SCALE linear scale 0 to 1. corresponds to the entire soundfile duration. If this is set to 0.5, the highest numbered voice will be half of the soundfile duration ahead of the lowest voice.
ABBREVIATION l->s PARAMETER Modulation of soundfile traversal speed by loudness DESCRIPTION Determines the degree of influence of the loudness sensor on soundfile traversal speed. If positive value are given, loud parts will be traversed FASTER and low parts will be traversed SLOWER. The opposite realtion holds for negative values. A referece value for loudness is given by THRESHOLD. See also the desription of the THRES parameter. UNITS / SCALE some kind of dB scale. 0 is no modulation.
PARAMETER GROUP Grain Duration ______________
INTRODUCTION These parameters determine the duration of grains. Generally, grains are too short to exhibit any inner structure, i.e. shorter than 20 ms. In many cases, grain duration will have an effect on the pitch percept, and on the "amplitude modulation"-effect. Long grains are computation intensive. You may need to increase grain distance values (see below) or decrease the number of voices when using long grains.
ABBREVIATION drFX PARAMETER Duration fix value DESCRIPTION minimum duration of grains. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the duration fix value.
ABBREVIATION drRG PARAMETER Duration random deviation range DESCRIPTION Range of a random noise source that will add some deviation to the grain duration fix value. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the duration random deviation range value.
ABBREVIATION drSP PARAMETER Duration spreading factor DESCRIPTION Grain durations can be spread among voices to create a chorusing effect or chords. This parameter determines the extent of spreading. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the duration spreading factor.
ABBREVIATION l->s PARAMETER Modulation of grain duration by loudness DESCRIPTION Determines the degree of influence of the loudness sensor on grain duration. If positive value are given, loud parts will be played back with longer grains and low parts will be played back with shorter grains. The opposite realtion holds for negative values. A referece value for loudness is given by THRESHOLD. See also the desription of the THRES parameter. UNITS / SCALE some kind of dB scale. 0 is no modulation.
PARAMETER GROUP Grain Distance ______________
INTRODUCTION These parameters determine the distance between grains. If no distance is given, than successive grains in one voice OVERLAP; when a fourth of a grain's duration is over, its successor grain will start. In this case (no distance), there will allways be four grains in one voice sounding at the same time. If soundfile traversal speed is set to 1 (with all modulations disabled) this setting will play back the original soundfile unaltered. Increasing grain distances frees up voices. Consider that many voices with rather long grain distances can produce equal densities (grains per second) as one voice with overlapping grains, but with a sensation of simultaneous, quasi-synchronous movement.
ABBREVIATION dtFX PARAMETER Distance fix value DESCRIPTION minimum distance between grains. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the distance fix value. The smallest distance is 1/4 grain duration, yielding an overlap of four grains in each voice.
ABBREVIATION dtRG PARAMETER Distance random deviation range DESCRIPTION Range of a random noise source that will add some deviation to the grain distance fix value. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the distance random deviation range value.
ABBREVIATION drSP PARAMETER Distance spreading factor DESCRIPTION Grain distances can be spread among voices to create a chorusing effect or chords. This parameter determines the extent of spreading. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the distance spreading factor.
PARAMETER GROUP Pitch / Transposition _____________________
INTRODUCTION The content of a grain, i.e. the excerpt of the input soundfile, can be trans- posed upwards or downwards by playback-speed variation (samplerate conversion). Mind the distinction between the speed of the global input soundfile index, which determines the input soundfile excerpts that grains are made of, and the speed of playback of the excerpts themselves. When both values deviate, there will be some sort of pitch independent speed change or the opposite.
ABBREVIATION ptFX PARAMETER pitch / transposition fix value DESCRIPTION minimum transposition of grain contents. UNITS / SCALE a factor for transposition. 1 is unmodified, 0 is indefinetly slow playback speed, 2 is an octave obove, 3 is the second overtone, i.e. an octave plus a perfect fifth. negative values indicate reversed playback.
ABBREVIATION ptRG PARAMETER pitch deviation range DESCRIPTION Range of a random noise source that will add some deviation to the grain transposition fix value. UNITS / SCALE Same as ptFX.
ABBREVIATION drSP PARAMETER Pitch spreading factor DESCRIPTION Grain transposition can be spread among voices to create a chorusing effect or chords. This parameter determines the extent of spreading. UNITS / SCALE Same as ptFX.
PARAMETER GROUP Miscallaneous and Dynamics __________________________
ABBREVIATION novc PARAMETER number of voices DESCRIPTION the number of parallel, quasi-synchronous grain streams. When only one voice is used, output will be mono. With more than one voice, even numbered voices will be output only on the left channel, and odd numbered voices will be output only on the right channel, allowing for 100% decorrelated stereo channels. UNITS / SCALE the integer part of the number gives the number of voices.
ABBREVIATION fdbk PARAMETER feedback DESCRIPTION an attenuated copy of the previous grain can be added to the current grain before output. This parameter determines the amount of feedback. The effect is that of a recirculating delay line, with the delay time determined by grain duration and grain distance. Yields comb-filter / "resonating chord" effects for pitch- period-scale grain times. The envelope follower is measuring the sum of the input signal from the input soundfile and the feedback signal; the compander can be therefore be used to avoid distortion with high feed- back values. In fact, it contols the ratio between input signal and feedback signal, and can be used to alter the static character of the feedback system. See also description for RATIO and for TRES. UNITS / SCALE a factor. Zero is no feedback, 1 is 100% feedback.
ABBREVIATION tres PARAMETER threshold DESCRIPTION controls envelope follower operation. A grain's peak value is determined before sending the grain to the audio output. This peak value is related to the "loudness" of the input soundfile at the current readout position. This "envelope" follower can be used to modulate the program's behaviour in a variety of ways: - to modify dynamics in a compressor / expander fashion (see RATIO parameter description) - to modify the speed of the global soundfile index (see l->s parameter description) - to modify the duration of grains (see l->d parameter description) the threshold is a kind of reference value for envelope follower modulations: in dynamics modification it determines the input level where amplification will be at a maximum, in speed and duration modulation, modulation will be positive or negative depending on whether the current input level is below or above this threshold. Consider that input level tracking is coupled with grain sizes; large grain sizes will "smear out" detail in the input signal's envelope, as the envelope is averaged over a wider time-span. UNITS / SCALE Arbitrary (0 to 1). The initial value is the peak value of the complete input soundfile. There is no point in higher threshold values. Envelope follower modulations get more extreme when DEcreasing this value!
ABBREVIATION rtio PARAMETER compression / expansion ratio DESCRIPTION determines the amount of dynamics modification. Ratio is the the degree of amplification to be applied to signals at "threshold" (see above description) level. the degree of amplification for signals below threshold level will vary linearly from 1 (no amplification) to ratio; as signal level grows from threshold level to maximum level, amplification decreases linearly, and is 1 (no amplification) for maximum input signals. Again: threshold defines the position of the compander "knee" and ratio determines the extent of compression (positive values) or expansion (negative values). With very small grain size, increased ratios and low thresholds the signal will look and sound more "rectanglular", effecting in some kind of distortion effect. UNITS / SCALE Arbitrary; 0 is no dynamics alteration. With a setting of 1 for this parameter, each grain will be boosted to be at maximimum level.
ABBREVIATION amp PARAMETER amplitude scaling DESCRIPTION a simple amplitude scaling factor for the ouput signal. When many grains overlap, it may be necessary to reduce output amplitude to avoid clipping (especially so when using high compression ratios). UNITS / SCALE A factor ranging from 0 (silence) to 4.
ABBREVIATION slew PARAMETER parameter slewing time DESCRIPTION determines the "inertia" of all other parameters. With large values for slew time, rapid movements with the mouse will be "smeared"; a parameter's actual value will slowly approach the value that has been set with the mouse or that has been recalled from a preset. The current slew time is stored with a preset; if presets are recalled in a sequence, each preset will be recalled with the slew time that was recorded with it, i.e. it will take that slew time to get from the current set of values to the set that is being recalled. Holding the left "alternate" button while recalling a preset will keep the current slew time instead of updating it with the value stored with the preset. Mind that changes of the POSITION parameter with some slew time and zero loop length (DEV) will have the same effect as cycling through the soundfile in a loop with some speed. In fact, both kinds of movements can be used together. The "inner movement" inside the loop is constrained by the position and deviation parameters (loop start and loop length) that are both subject to the slewing process. It is possible to create rather complex paths through the input soundfile this way. UNITS / SCALE logarithmic scale that corresponds to the tempered pitch scale. Increasing this value by 12 will double the slew time.
________________________________________________________________________________
This is software under development.
Coming up soon: - amplitude dependent synchronisation of voices - knobs with virtual masses and frictions - user interface improvements (better waveform display, better faders, visual feedback) - breakpoint-envelope editing of parameter movements - ordering grains by acoustic similarity ... Should you happen to fund projects like this or know someone who does, let me know.
For questions, comments and suggestions, please contact:
Gerhard Behles
The Electronic Studio at Technical University Berlin Mail Einsteinufer
17, D - 10587 Berlin Tel ++49 30 314 22821 / 25557 Fax ++49 30 314 21143
Email gb@gigant.kgw.tu-berlin.de
8. Einführung in das physikalische Modelling
8.1 Beispiel der Verschaltung einer Flöte
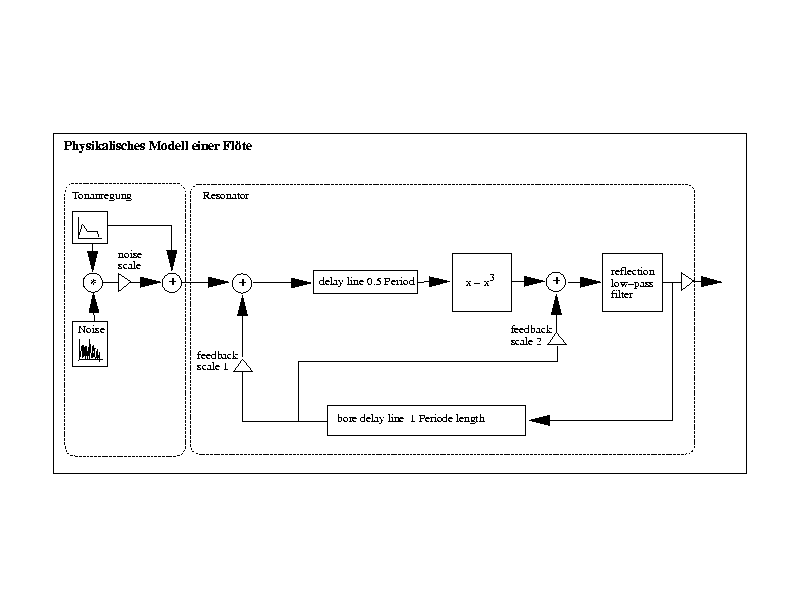
Neben dem obigen Beispiel der Flute (flute.ins) gibt es in CLM noch piano.ins, singer.ins.
8.2. Beispiele phyikalischer Modelle mithilfe eines modularen Modelles.
Abstract:
Genesis is a software package driven by the physical modelling language "Cordis Anima" (Claude Cadoz, Anni Luciani, Jean Loup Florens. See Proceedings ICMC 1995 Banff, Computer Music Journal 17.1)
Cordis Anima is a generalized approach to physical modelling. It uses generalized particle physics paradigms based on the physical ineraction between punctual masses. These masses are linked to each other and perform linear elastic and viscous interactions combined with finite-state automata processes alowing the describiton of any kind of non linear interaction. One can build interaction like articulated objects, collisions, dry friction, adherence, sticking...
Some software functions and a GUI is added to create a software which feeds the specific needs of people working in music and acoustic. For example, the movement of some masses can be monitored and written to a floating point soundfile. The soundfile then appears in a soundeditor where it can be listened and modified.
Besides these tools for handling audio data an animation procedure is available. The Animation shows the action of the current patch in a very much slower speed then the actual structure vibrates. This is done to make it a tool for understanding the interaction between the vibrating structures.
The talk will explain the approach of using a GUI for physical modelling as well as showing some patches for discussing the different problems occuring while working with physical modells as a compositional tool.
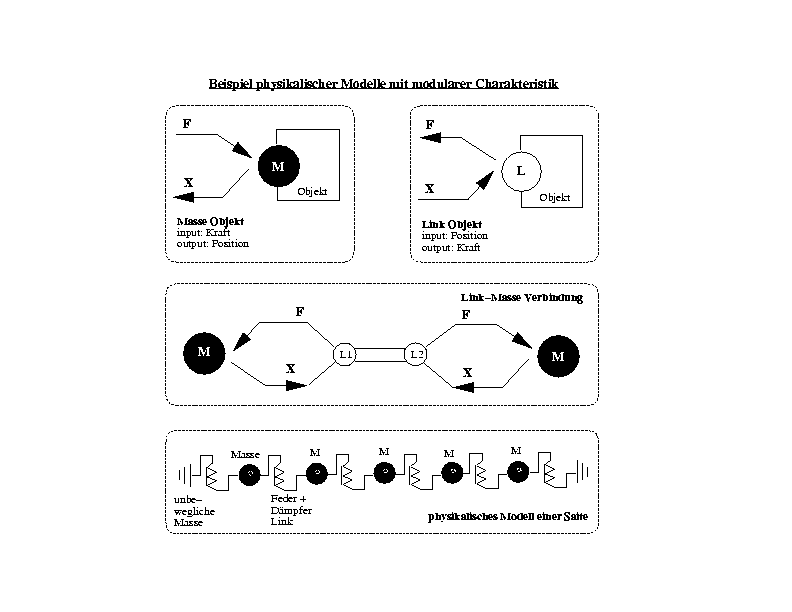
8.3 The theory behind cordis anima
The approach of the Cordis anima using particle physics for creating complex physical modells is ruled by the paradigm of the interaction of punctual masses. This means equivalent to the physical existence of substances that single molecule like units create the frame of a physical object. These molecule like units which I refer to as masses are linked together to create an interaction which represents the flow of different types of power between the masses. The connection between the punctual masses is installed with links. These links perform a translation of the power type.
Lets say one mass is pulled while being connected to other masses with a link. The force of pulling the mass would cause it to perform a displacement. The displacement of the mass hass a consequence onto the other masses since the masses are connected through links. One type of connection the elastic aspect. Has the link an elastic charakter, the displacement of the one mass will have a consequence toward the elastic link, since it is now stretched or squeezed. The displacement is translated into force. This force is then translated in the link to a displacement of the other mass or masses. The link
There are 2 basic ways to inject energy into the system which of course has no intial envergy: Displacing a Mass or injection Energy into a Link. There are several ways of performing this task.
1. by Displacement of a Mass 2. by an initial force 3. by an interactive force performed with a conditional link 4. by injection of an initial force into the link 5. by injection of a variable force or displacement via the gesture technique.
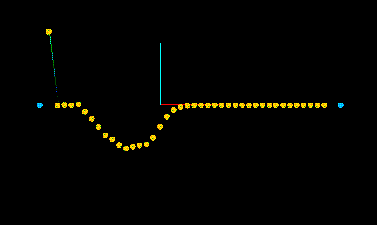
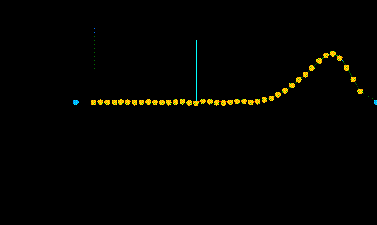
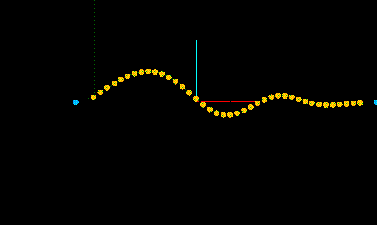
Conditional link: The normal link reproduces a linear mapping between the 2 possible parameter: f.e. the higher the input force given a specific elasticity or viscosity the higher the output force. The conditional link applies fields of nonlinear behaviour between these value fields. For example the following characteristic would cause the link to break if the applied force would increase a specific value.
input force ..../| ../ .| / ...|______output force or position delta
"which allows to move one or more points of the structure out of the balance position, and then to release the link when the tensed force exceeds a predetermined threshold." {this is similar to a plucked string] "The second assumes a minimal modelisation of a striker, made of one or several masses carried along by a function of gestural command,m and linked at the structure exitaition points by an interaction conditional link. (ICMC Proceedings 1994 Page 16/17).
Mp'' + Zp' + Kp = F
M=intertia (Traegheit) Z=viscosity K=elastisity F=external force p' and p'' are the first and second derivates of the postion p.
Since the network of interaction is created by separate link and Mass Modules it is possible to apply complex parameter modification to each desired element of the network.
Application of a
A special form represents the conditional link which can functions in specific circumstances. It allows to include friction as a specific way to transmit energy. A bow f.e. has moments where the string and the hair create solid connection followed by a short time segment where the string slips and the bow is separated from the string. This effect could be created with a conditional link which allows the delivery of energy from one mass to the other only until a threshold of movement or distance is reached.
Since the space of the masses and its links is one dimensional, the representation of the position of the mass is not equivalent to the 3 dimensional position the mass has in the simulation. This means that the model does not take in advance geometric aspects like angle.
What especially is interesting in the resulting sound out of such a physical modell is the fact its natural behavaior and as well its possibillities of modification. Usually a sound if it is created in an artifical manor its modification shows some artefacts of the synthesis method.
These elements will in all case of decomposition be a physical modell and behave like one. The modification of the patch and the destruction of links and masses will not destroy the functionality of the system. Since can be explained by the fundamental type of the structure of this model. Since all the elements got a very general charackter, the decomposition does not destroy aspects of the functionalism as a physical object.
A more specific model with separate function modules works only in special circumstances and parameter constellations simular to physical reality.
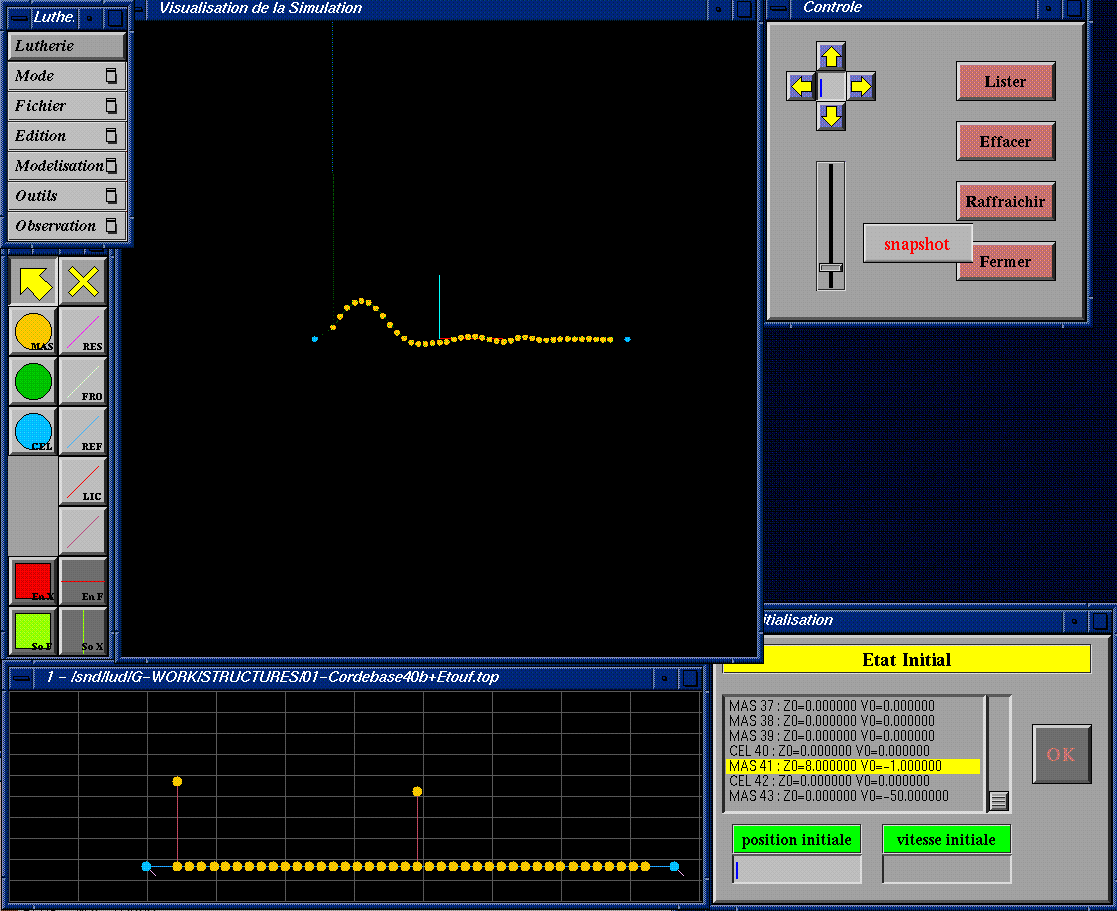
snap.gif
snap4
snap5
snap6
snap7
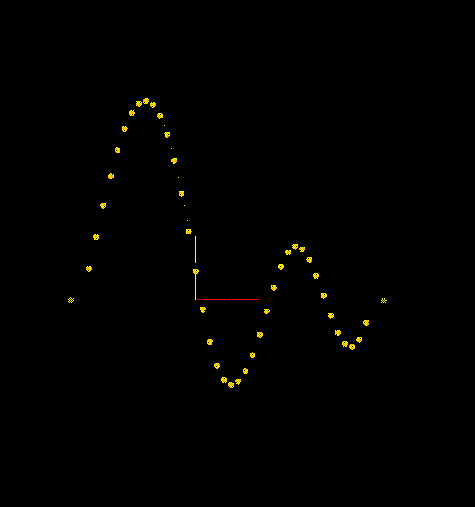
snap2b
snap3
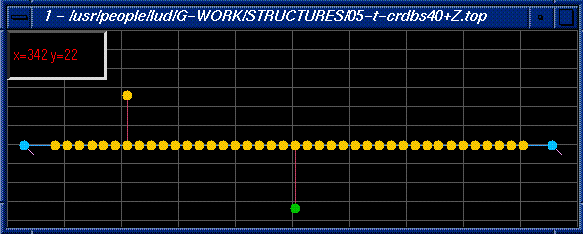
05-t-cordbs40
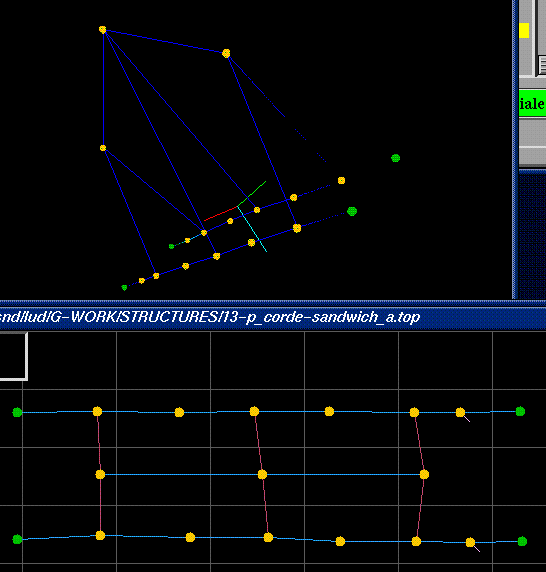
13-p
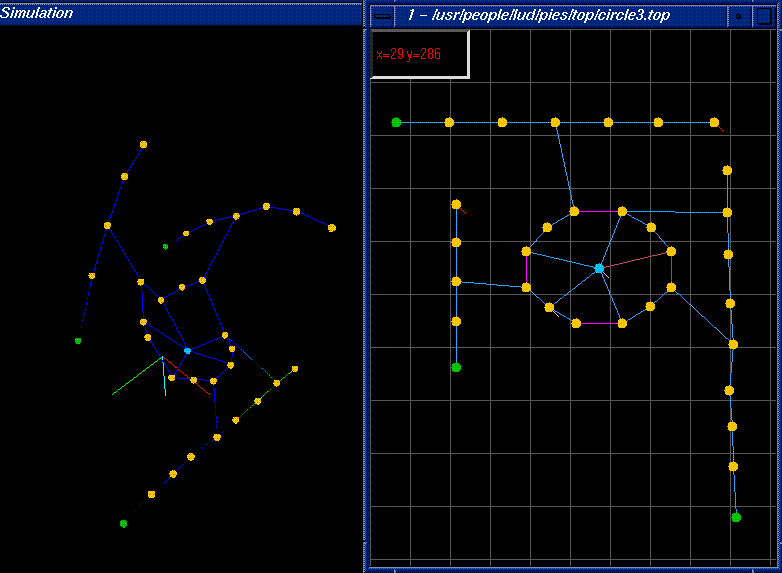
circle3
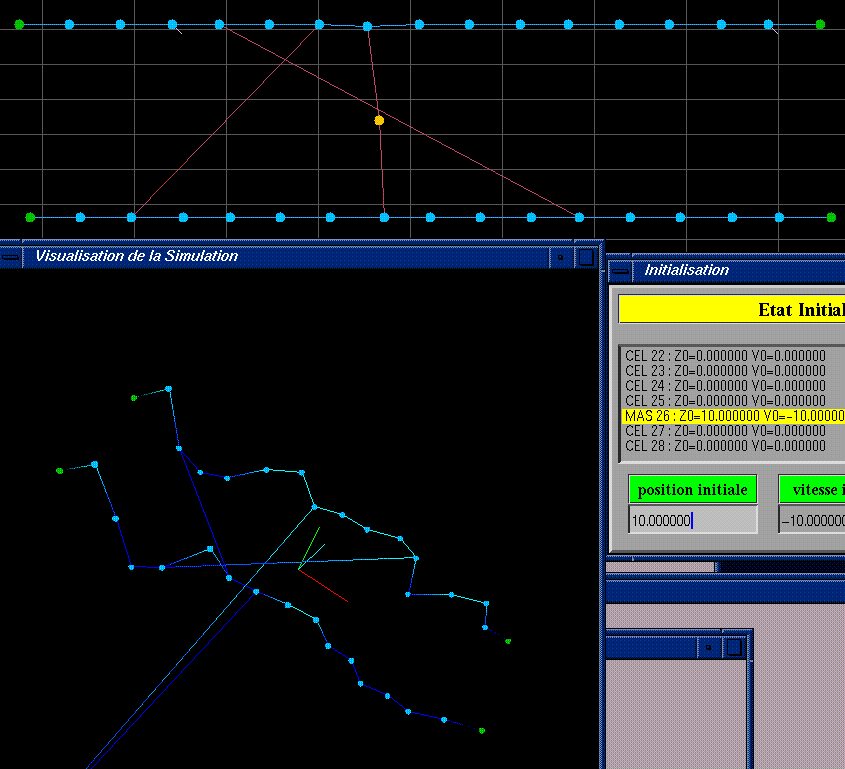
d-string
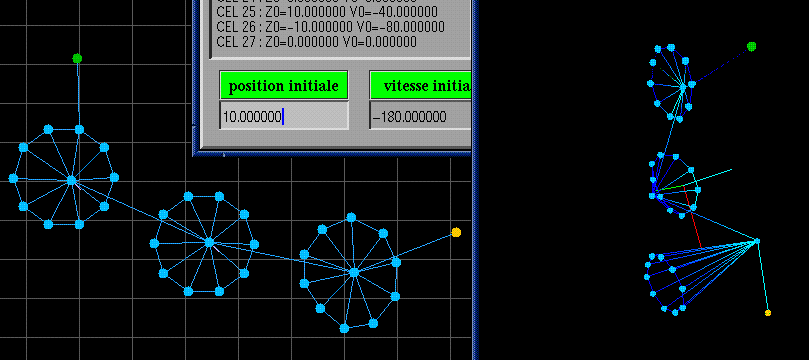
plates2
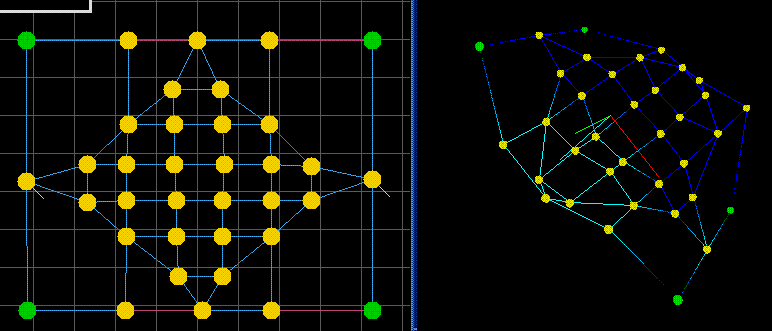
square26
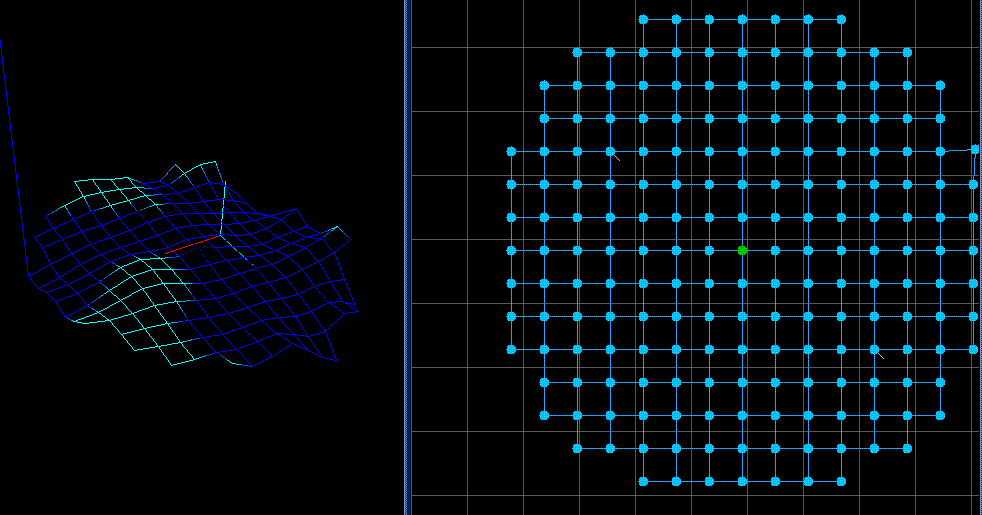
membrane
9. Diskussionspunke: elektronische Musik
Die Grenzen loesen sich auf.
In der Vergangenheit der Computermusik entwickelten sich immer wieder verschiedene Moglichkeiten mit dem Computer Musik zu machen, die zu neuen Wegen der Interaktion zwischen Hoerer und Musik, zwischen Bild und Ton, zwischen Klang und Raum, zwischen musikalischer Sprache und Environment fuehren. Dabei naehern sich die visuellen und die akustischen Kuenste, durch das von ihnen verwendete Arbeitsmittel, aneinander an.
Obwohl sich die verschiedenen Kunstformen mit einem jeweils anderen Medium befasst, sprechen alle diese Kunstformen, die den Computer als mittel zur Realisierung ihrer Ideen benutzen in dem Moment die gleiche Sprache, in dem sie die Maschine programmieren. Egal welches Kunstwerk mit dem Computer geschafffen werden soll, alle Kuenstler sprechen hier in einer Maschinensprache in der sie Probleme in Teile zerlegen und zu sequenziellen Programmablaeufen zusammenfuegen. Deswegen macht es Sinn so unterschiedliche Kunstrichtungen, wie Animation Interacitve Art, World Wide Web und Musik in der Ars Electronica zu vereinen. Die Annaeherung zwischen den Sparten geht sogar so weit, dasse einige Werke in mehrere dieser vier Kathegorien gleichzeitig hineingehoerten.
Troz dieser Gemeinsamkeit gibt es jedoch einen Moment, in dem sich die Uebereinstimmungen zwischen den verschiedenen Kunstformen trennt: Der Moment, in dem sich entscheidet mit welcher Frequenz die errechneten Daten analogisiert werden. Hier entscheidet sich, welche Wahrnehmungsmechanismen des Menschen mit ihren doch recht unterschiedlichen Faehigkeiten angesprochen werden. Hier trennt sich die akustische Sprache (akustische Kunst) von der visuellen Sprache. Die Konsequenzen dieser Entscheidung betreffen aber nicht nur die Organe, mit denen die Objekte wahrgenommen werden, sondern haben auch Auswirkungen auf die Qualitaet der Wahrnehmung. Die Abstraktionsfaehigkeit, die Komplexitaet, die Emotionalitaet der akustischen Wahrnehmung unterscheidet sich signifikant von den Faehigkeiten der visuellen Wahrnehmung. Versuchen Sie mal das Thema von Beethovens 5. mit Worten zu beschreiben oder das Ars Electronica Center Emblem und sie werden feststellen wie unterschiedlich das akustische Abstraktionisvermoegen von dem Abstraktionsvermoegen visueller Eindruecke ist. Diese Tatsache hat konkrete Auswirkungen auf die Inhalte und die Ansprueche an die jeweilige Kunstform, die sich konsequenterweise sehr voneinander unterscheiden.
Was erwartet man demzufolge von neuer Computermusik? Muessen diese Stuecke jederzeit spektakulaer sein, immer neue Klangfarben praesentieren immer schriller extremer aufregender sein und immer neueste technologische Mittel bemuehen? Gehorcht die Kunst solchen Forderungen, oder sollten solch ein kuenstlerisches Verhalten nicht eher ein Ergebnis von aesthetischen Reaktionen auf eine spezifische Situation, also ein Reaktion auf kuenstlerische Beduerfnisse sein?
Hierbei moechte ich die Bedeutung der Verwendung von digitalen Technologie in der Musik in Bezug auf den oben geaeusserten Anspruch ein wenig erlaeutern.
Warum hat die Einfuehrung sogenannter neuer Technologien, d.h. die digitale Bearbeitung und Erzeugung von Klaengen mit dem Computer, nicht die erwartete ganz neue Art von Musik zur Folge gehabt? Bei der Einfuehrung digitalen Technologie muss man zwischen quantitativen und qualitativen Fortschritten unterscheiden. Viele Erfindungen, wie die des analogen Oszillators, die eines analogen Filters, die eines Speichermediums waren eindeutig qualitativer Natur. Es gab vorher nichts Aequivalentes und deswegen konnten diese technischen Innovationen auch zu neuen expressiven Moeglichkeiten fuehren. Viele, als Fortschritt erscheinende Moeglichkeiten der digitalen Technologie stellen in Bezug zur Vergangenheit gesehen aber nur eine quantitative Veraenderung dar: Das Sampling, die verschiedenen Synthesemethoden, die Phase Vocoder Technologie, das Mischen und Schneiden usw. Zugegeben, es lassen sich viele Dinge genauer und schneller machen. Das an sich ist sicherlich schon eine Qualitaet, aber welche Konsequenzen hat diese Qualitaet fuer die mit ihr entwickelte Musik?
Die ganze Sampling Technologie z.B. ist nicht neu. Alle dort benutzten Bearbeitungsschritte kann man schon in der Musique Concrete Pierre Schaeffers mit analogen Mitteln angewendet hoeren. Was neu ist, ist die Praezision und Geschwindigkeit mit der die Arbeitsprozesse ausgefuehrt werden koennen. Das ist sicherlich ein Grund fuer die Popularitaet dieser Technik, waehrend ein anderer Grund allerdings in den aesthetischen Praemissen der Postmoderne zu finden sind. Betrachtet man die technologischen Veraenderungen der letzten Jahre unter diesem Erkenntnisstand, so entsteht die Frage, was sich eigentlich veraendert hat? Das Problem ist, dass die digitale Revolution aus den oben beschriebenen Gruenden mehr die Qualitaetssicherung steigerte, das Produktionstempo beschleunigte, die Arbeitsmittel verbilligte und ein hoeheres Mass an Praezision ermoeglichte. Aus diesen Veraenderngen entstehen nicht unbedingt neue aesthetisch/kuenstlerische Fragen und auch nicht unbedingt neue Antworten.
Musikalisch gesehen benutzen die meisten Komponisten die digitale Technologie ebenso, wie sie analoge Technologien genutzt haetten. Kein Wunder, dass sich die aesthetische Entwicklung nach anderen Kriterien als denen der neuen leistungsstarken Herrstellungstechnik orientiert und die Entstehung neuer Qualitaeten keinen nachhaltigen Schub erhalten hat. Setzt man die Granularsynthese z.B. als eine typische digitale Errungenschaft an, also eine Technik in der ein existierender Klang in kleinste Stueckchen aufgesplittert wird, so laesst sich hier auch nur konstatieren, dass diese Synthesetechnik selber nicht neu ist und schon vorher mit analogen Sample and Hold Generatoren oder einer komplexen Bandschneidetechnik praktiziert worden ist. Was neu ist, ist wiederum nur das einfachere Handling und die Geschwindigkeit, mit der diese Prozesse durchgefuehrt werden koennen.
Die Errungenschaften der digitalen Technologie stellen aber um so dringlicher die Frage nach der musikalischen Intention und nach den Inhalten. Gerade, wo die Kreativitaet durch die massenhafte Verbreitung von Produktionsmitteln auf eine grosse Schar von Komponisten verteilt worden ist, sollte man erwarten, dass sich unterschiedlichere Fragestellungen und unterschiedlichere Antworten entwickeln als es der Fall ist. Man sollte aber nicht unbedingt erwarten, dass sich jetzt tausende lauter kleine Stockhausens und Rissets vor den Computern tummeln und eine Revolution nach der anfachen. ?hnlich, wie in der Wissenschaft laesst sich hier konstatieren: je mehr geforscht wird, desto weniger Spektakulaere bahnbrechende Erkenntnisse werden zutage gefoerdert. Die vielen gewonnenen Erkenntnisse verhalten sich ganz im Gegenteil, wie das Hinzufuegen von vielen neuen Kleinen Aspekten zu einem groesseren Ganzen.
Die Beschleunigung und leichtere Handhabung der Technologie hat allerdings auch ein veraendertes Verhalten der Komponisten waehrend des Kompositionsprozesses zur Folge. Ist der Aufwand sehr gross, d.h. die Zeitspanne der Realisierung eines Werkes sehr lang, so fliessen in dieser Zeit zweifelsohne sehr viele Details in die Konzeption eines Werkes hinein, die bei der Realisierung innerhalb eines kurzen Zeitraumes kaum erdacht werden koennten. Der Widerstand, den ein Medium dem Komponisten entgegenbringt, erzeugt aber ausserdem eine klare musikalische Motivation oder Intention fuer die Komposition. Werden die Probleme bei der Realisierung einer Komposition geringer, so heisst das nicht, dass es dadurch einfacher wird eine gute Musik zu realisieren.
Die digitale Technik hat in ihrem Bestreben Wiederstaende zu beseitigen auch einige negative Konsequenzen bezueglich der Ansprueche an die Komponisten und Kompositionen. Nicht nur, dass der Praezisionsstandard steigt und die Toleranz gegenueber Qualitaetsmaengeln sinkt, was ja zunaechst sehr positiv ist, zusaetzlich wird der Anspuch an die Komponisten ein Werk fertigzustellen sehr eingeengt. Als Beispiel will ich hier anfuehren, dass Stockhausen fuer die Realisierung von Kontakte meines Wissen nach ueber ein Jahr im WDR Studio arbeiten und experimentieren konnte. Heutzutage werden Realisierungsstipendien vergeben, die die Fertigstellung des Werkes innerhalb eines Zeitraumes von 1 Monat wuenschen.
Wie laesst sich aber die Frage nach der Qualitaet elektroakustischer Musik stellen. Laesst sie sich aehnlich wie in der instrumentalen Musik stellen oder spielen hier andere kompositorische Intention ein Rolle? Augenfaellig wird hierbei die haeufig vorkommenden etuedenhaften Werke von kompositorisch interessierten Technikern, die den kompositorisch motivierten Stuecken gegenueberstehen.
Bezueglich der Frage nach dem unterschiedlichen Niveau zwischen der technologischen und aesthetischen Entwicklung einzelner Stuecke elektroakustischer Musik laesst sich aber keine allgemeine Antwort geben, sondern eher eine, die jedes Stueck in eine Bandbreite zwischen kompositorisch oder technologisch motivierten Werke einordnet: Je mehr ein technologisches und kein musikalisches Interesse im Vordergrund steht, desto weniger musikalisch interessant ist das Ergebnis. Unmoeglich zu beurteilen ist aber die Moeglichkeit der aesthetischen Innovation durch solche Stuecke. Schliesslich wurden viele Komponisten durch die technologische Innovation und deren erste aesthetische Evaluation beeinflusst. Man sollte in der Beurteilung solcher Stuecke vorsichtig sein, da sie ein Potential beisitzen koennen, das sich sehr indirekt auf Komponisten auswirken koennen.
Es laesst sich also konstatieren, dass neue Technologie nicht unbedingt zu einer neuen Musik fuehrt, sondern aesthetische Kriterien und Beduerfnisse eher dazu geeignet sind, die musikalische Sprache weiterzuentwickeln.
Pierre Schaeffer z.B. war einer der ersten, der die Klaenge systematisch kathegorisierte und in eine Art Datenbank einordnete. Durch diese Kathegorisierung hat er gleichzeitig ein Instrumentarium fuer die Bewertung solcher Phaenomene wie Klangfarbe und Struktur sowie deren Interaktion entwickelt. Anhand von Schaeffers Beispiel laesst sich deutlich zeigen, dass fuer ihn die musikalischen Kriterien wichtiger sein sollten als die technologischen. Was nuetzen technologische Moeglichkeiten, wenn sie nicht zum Sprechen gebracht werden? Hier zeigt sich, dass die Weiterentwicklung einer musikalischen Sprache auch in Bezug auf die damit einhergehenden langsameren aufeinander aufbauenden Entwicklungstadien, Sinn macht und Voraussetzungen fuer eine funktionierende Musik schafft.
Als Ausblick bezueglich technologischer Entwicklungen bleibt abzuwarten, welche qualitativen Einfluesse zukuenftige technologische Entwicklungen auf die musikalische Aesthetik und Sprache haben werden. Schliesslich werden auch einige qualitiv wirklich neue Techniken darunter sein. Der naechste zu erwartende Entwicklungsschub in der Computermusik koennte vielleicht von einer Technologie erfolgen, die es schon gibt, die jedoch kaum in Kompositionen elektroakustischer Musik eingesetzt worden ist: das physikalische Modell als Virtual Reality Instrument. Allerdings darf man die Erwartungen erfahrungsgemaess nicht zu hoch schrauben. Spiegelt das physical Modelling in vielen Aspekten doch nur die physikalische Wirklichkeit und somit keine qualitativ neuen Erfahrungen wieder. Interessant in diesem Zusammenhang, ist, dass viele, sehr aufregende Techniken, wie neuronale Netze, genetische Algorithmen, gewiss nicht ohne Grund, wenig benutzte Mittel der Klang- oder Struktursynthese darstellen. Wie sich der Gebrauch von physikalischen Modellen in der Zukunft entwickelt, darauf kann man noch gespannt sein.
bell.ins ein Instrument
fmex.ins mit einer anderen fm-bell, mit einer fm-drum und einem gong.
Konzert 1
Iannis Xenakis Orient - Occident 1960 10'56
William Schottstaedt Water Music I 1988 10'14
John Chowning Turenas ca 1972 9'54
Ludger Brümmer Ambre, Lilac 1995 21'45
Francesco Boschetto Trasumanar 1996 11'06
Regis Renouard Lariviere Futaie 1996 14'03
Gilles Gobeil Le Vertige Inconnu 1993 8'23
Ludger Brümmer Phrenos 1996 18'45
Dickreiter, Michael; Handbuch der Tonstudiotechnik. Bd.1 und Bd.2, K.G. Saur 1987
Moore, F. Richard; Elements of Computer Music. Prentice Hall 1990
Penrose, Roger; Computerdenken. Spektrum der Wissenschaft Verlag, Heidelberg 1991.
Steller, Erwin; Computer und Kunst. B I Wissenschaftsverlag Mannheim
1992
sonstige Topics
Brümmer, Ludger: Zur
Interface Problematik
CLM
und CM aus der Sicht des Komponisten
Using a digital Sound Synthesis language in composition; Computer Music
Journal
vol 18 Nr 4, MIT Press 1994
Ludger Brümmer_______________________________________________________
Copyright 1997 by Ludger Brümmer_________________________________________Auszüge
und Zitate dürfen nur mit Angabe von Text und Autor benutzt werden.