Klänge nach den Gesetzen der Natur

Ludger Brümmer  ZKM 8.5.1998
Copyright 1998

1. Einleitung: physical Modeling


Seitdem der Mensch denkt, hat er ein Bedürfnis nach Abstraktion entwickelt. Das läßt sich schon in den Werken der frühesten Kulturen erkennen.

Abstraktion [lat.], die Bildung von Begriffen, d. h. die von den vielfältigen Erscheinungsweisen eines Dinges absehende (abstrahierende) Benennung der allg. Gesetzmäßigkeit bzw. des Wesentlichen, das als solches nicht sichtbar ist, sondern nur als Phänomen, das den Erscheinungen gemeinsam ist, gedacht
werden kann. (Meyers Lexikon)

Kann man Abstraktion vielleicht als den Vorgang des menschlichen Denkens bezeichnen, der ihm ermöglicht Vorgänge und Sachverhalte überhaupt zu begreifen. Denn ohne Zweifel steckt in jeder Abstraktion ein modellhaftes Rekonstruieren von Wirklichkeit.

Die Wirklichkeit selber können wir nicht wahrnehmen, da wir ja noch nicht einmal wissen, wie das, was die Sinnesorgane wahrnehmen in Wirklichkeit ist und jeder dieser Reize einen durch das Gehirn hergestellten, also an sich schon modellhaften Eindruck hinterläßt.
Da uns das Phänomen der Abstraktion von der ersten Sekunde unserer Existenz bis zur Letzten begleitet, sollte es nicht verwundern, daß sich der Prozeß der Abstraktion nicht nur auf das Verständnis von Gegebenheiten bezieht, sondern, daß die ermittelten Erkenntnisse über einen Sachverhalt dazu benutzt werden, diesen zu rekonstruieren.
Eine Rekonstruktion ist demnach ein Mechanismus, der den zu rekonstruierenden Gegenstand abbildet und versucht, ihm in seinen Eigenschaften möglichst ähnlich zu sein. Ein Modell ist solch eine Rekonstruktion, die allerdings impliziert, dem Original nur in einige wesentlichen Punkten zu entsprechen.
Ein physikalisches Modell ist dementsprechend der Versuch, einige Aspekt der Wirklichkeit mit Hilfe eines modellhaften Regelsystems innerhalb eines abstrakten Raumes abzubilden.
Konkret entsprechen die mathematischen Beschreibungen einem solchen Regelsystem, während die Aktivierung dieses Regelsystems innerhalb einer Software Simulation einen abstrakten Raum darstellt.

Dieser abstrakte Raum des physikalischen Modells ist, und das macht das Modellhafte so interessant, jederzeit reproduzierbar und in definierter Art und Weise manipulierbar.

1.2 was war die Motivation für die Entwicklung physikalischer Modelle in der Musik?


Seitdem es Musik gibt, gibt es einen Entwicklungprozeß innerhalb der Klangerzeuger. Ausgehend von den verschiedenen Arten, die Stimme zu benutzen wurden im laufe der historischen Entwicklung Instrumente zu Klangerzeugung eingesetzt und kontinuierlich modifiziert.
In der sogenannten instrumentalen Welt der Musik haben sich aber im Laufe der Zeit einige Klangideale, bzw. Definitionen von Klangidealen entwickelt, die sich gefestigt und in ihrer Entwicklungsgeschwindigkeit reduziert haben. Der Klavierklang, der Geigenklang, der Gitarrenklang entspricht heutzutage einer noch nie zuvor so streng gewesenen Normierung. Mit gutem Grund versuchten Komponisten, gemäß einer historischen Reduktion der Vielfalt, der engen Klangdefinition der heutigen Instrumente durch immer ungewöhnlichere Spieltechniken entgegenzuwirken. Das Paradoxon ist aber, daß auch diese Komponisten als Voraussetzung für ihre Spieltechniken, die exakte Normierung des Instrumentes fordern und aktiv voran treiben.
Die Entwicklung von Klangmaschinen bzw. Instrumenten hat sich im Laufe der Zeit auf den Bereich der elektronischen Musik verlagert. Sicherlich mit gutem Grund. Einerseits wurde der Computer immer mehr zu einem verfügbaren Arbeitsmittel. Andererseits lassen sich aber auch viele Aspekte eines mit Software gebauten Instrumentes jederzeit reproduzieren, da sich der Trend zu einer normierten Entwicklungsumgebung hin durchsetzt hat.
Die Entwicklung physikalischer Modelle hat hierbei deckungsgleich mit den experimentellen Voraussetzungen stattgefunden. Die benötigte Leistungskraft der Computer geht einher mit einem größer werdenden Interesse an den theoretischen und statistischen Forschungsergebnissen wissenschaftlicher Untersuchung.
Die beiden Aspekte der elektronischen Musik, das Künstliche und das Natürliche haben aber immer gleichzeitig eine Rolle gespielt, was sich auch in dem Nebeneinander von sogenannter elektronischer Musik und Musique Concrete äußert.
Deshalb läßt sich das Interesse an der physikalischen Abbildung von Klangprozessen mit Hilfe des Computers erklären. Einerseits geht es hier um ein Erfassen und Benutzen von Wirklichkeit. Andererseits aber um die Verfremdung und Manipulierbarkeit der Wirklichkeit über die Grenzen des ansonsten mechanisch Möglichen hinaus.

1.3 Was hat sich durch die Einführung physikalischer Modelle verändert?


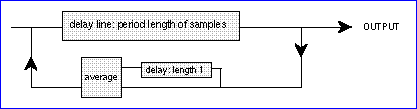
Für die Klangforscher hat die Einführung physikalischer Modelle im Wesentlichen Konsequenzen auf die Arbeitsumgebung gehabt.
Ästhetisch läßt sich allerdings noch wenig über die Auswirkung der zunehmenden Verfügbarkeit hochwertiger physikalischer Modelle sagen, da sich deren Verbreitung und Anwendung innerhalb der elektronische Musik erst seit einigen wenigen Jahren beobachten läßt

1.4 frühere Beispiele für physikalische Modelle: der Karplus Strong Algorithm

Ein frühes und sehr häufig benutztes Beispiel für ein natürliches Klangphänomen, das mit sehr einfachen mathematischen Methoden beschrieben werden kann stellt der Karplus Strong Algorithmus dar, der das Ausschwingungsverhalten einer Saite darzustellen im Stande ist. Um die Delay Loop mit Energie zu füllen werden die Samples mit Random Werten gefüllt und durchwandern die Averager und die 2 Delay Lines im Kreise. Die Filtergleichung des obigen Filters würde in etwas so aussehen:

 y n = xn - srate / freq + ((yn-1 + y) * .5)
 

1.5 ein komplexeres Beispiel für ein physikalisches Modell: 


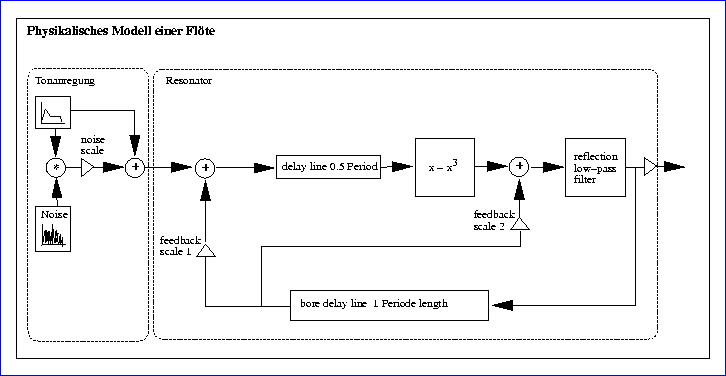
Das Funktionsschaltild einer Flöte von Perry R Cook. entwickelt im CCRMA der Stanford University

Perry Cook nennt seine Art physikalische Modelle herzustellen Physikal Inspired Modelling. Der Grund hierfür ist wohl in der Tatsache zu suchen, daß es sich bei seinem Typ von Modellen um abstrakte Systeme handelt, die komplexe Prozesse miteinander Verschalten, welche in Etwa der Realität entsprechen, jedoch keine physikalische Allgemeingültigkeit repräsentieren.
 

2. Das Cordis Anima Environment


2.1 Grundgesetze der Mechanik: Die Newtonschen Gesetze

1. Jeder Körper verharrt im Zustand der Ruhe oder der gleichförmigen, geradlinigen Bewegung, solange keine Kräfte auf ihn einwirken (Trägheitsgesetz).

2. Die Beschleunigung eines Körpers ist der einwirkenden Kraft proportional und ihr gleichgerichtet (dynam. Grundgesetz).

3. Übt ein Körper A auf einen Körper B eine Kraft F1 aus, so übt stets auch der Körper B auf den Körper A eine Kraft F2 aus, die von gleichem Betrage, aber entgegengesetzter Richtung ist, F1 =-F2 (Newtonsches Wechselwirkungsgesetz).

Festlegung: 1 N ist gleich der Kraft, die einem Körper der Masse 1 kg die Beschleunigung 1 m/s2 erteilt: 1 N = 1 kgm/s2.

 2.2. Die Funktionalität der Newtonschen Gesetze in Cordis Anima

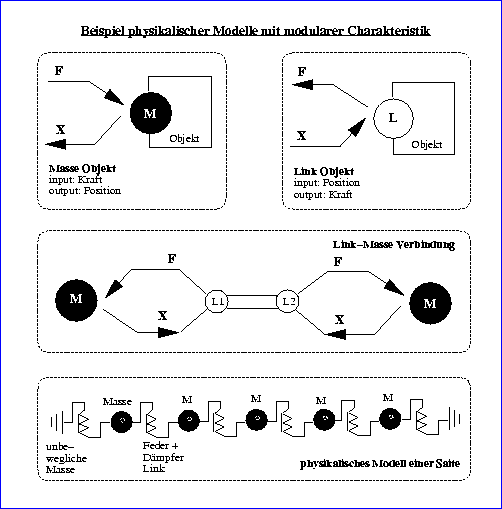
Gemäß der Newtonschen Gesetze gibt es in der Physik also die Größen: Kraft und Masse. Diese beiden Größen wirken sich in der Zeit aus. Dabei wird ein Teil der Kraft in andere Agregatzustände, wie z.B. Bewegung oder Wärme übersetzt. Dieser Kraftverlust wird in Cordis Anima durch den Parameter der Dämpfung simuliert.  Ein weiterer Aspekt der Verteilung der Kraft stellt der Aspekt der Zeit dar. Kraft breitet sich nicht nur im Raum aus, sondern auch in der Zeit. Diese Ausbreitung steht in Abhängigkeit von dem Medium, in dem sich die Kraft bewegt. Neben den Dämpfungseigenschaften zeigt jede Substanz auch eine spezifische Flexibilität. Es gibt dementsprechend harte bzw. starre und weiche, flexible Materie.
Ist ein Material starr, so wird sich die Kraft, einmal in das schwingenden System eingedrungen, sehr weit und lange verbreiten. Deshalb kann z.B. eine hohe Schwingungsgeschwindigeit erreicht werden.  Ein weiches Material hingegen schwingt williger ein, verbreitet die Kraft jedoch nicht so stark.
 

3. Das Patch als Definition der Klangcharakteristik

Eine schwingende Struktur besteht   aus 2 wesentlichen Elementen
1. Dem Element, das Kraft in die Struktur injiziert.
2. Der Struktur, die von dieser Kraft tangiert wird.
Es existiert also ein aktives und ein passives Element. Diese entsprechen in Etwa dem eines Hammers und einer Saite beim Klavier oder dem des Fingers und der Saite bei einer Gitarre.

Falls diese Schwingung nun hörbar gemacht werden soll, so spielt
3. die Art der Übertragung der Energie, der Ort der Abnahme, die Art der Umwandlung in
Luftschwingungen usw.
ebenfalls eine Rolle.

3.1 Sich bewegender Flächen


3.1.1 Das Gewicht der Elemente bestimmt die Geschwindigkeit der Bewegung.
 Schwere Elemente benötigen mehr Kraft zur Bewegung und werden demgemäß bei gleicher Kraft langsamer bewegt. Gleichzeitig reduziert sich inder Wirklichkeit auch der Weg der Bewegung. Dieses wird jedoch durch den Normalisierungsalgorithmus kompensiert, der die Lautstärke aller entstehenden Klänge immer auf 1 setzt.

3.1.2 Der k Wert bestimmt die Steifigkeit des Materials. Die Steifigkeit bestimmt, wie gut die Bewegung weitergeleitet wird. Ein Gummiband mit geringer Steifigkeit kann auf der einen Seite erheblich bewegt werden, wahrend von der Energie auf der anderen Saite kaum etwas ankommt. Anders jedoch ein Stahlstange, die schlägt man sie auf der einen Saite an, noch über eine große Distanz hin schwingt. Man kennt dieses Phänomen auch von der Eisenbahn, bei der die Schiene eine Bewegungsenergie über eine lange Strecke weiterleitet und hörbar macht.

3.1.3 Der z Wert bestimmt, wie schnell die Energie abgebaut wird. Ist der Wert hoch, so ist quasi zwischen jeder Masse ein kleiner Stoßdämpfer eingebaut, der die Energie schnell absorbiert. Das ist dann unabhängig von der Leitfähigkeit einer Materie.

Wasser zum Beispiel hat eine geringe Steifigkeit aber auch eine sehr geringe Absorptionfähigkeit von Energie. Deswegen breiten sich Wellen über einen so weiten Raum aus.
Luft hingegen hat eine viel höhere Absorption als Wasser.

3.2 Flow Charts schwingender Flächen


3.2.1 Summierung von Schwingungen und Kräften
Ähnlich wie in der herkömmlichen Synthesetechnik können verschiedene Schwingungen mit Hilfe der Links addiert oder abgeleitet werden. Werden verschiedene Kräfte mit einer Masse verbunden, so entspricht das in Etwas einer Addition, wobei nicht vergessen werden darf, dass die Links bidirektional arbeiten, d.h. daß die Verbindung von Elementen immer auch Auswirkungen auf den Sender der Kraft hat.
3.2.2 Teilung bzw. Differenzierung von Schwingungen und Überleitung auf andere schwingende Körper
Eine sogenannte Ableitung findet statt, wenn die Schwingung einer Fläche an einer bestimmten Stelle abgenommen und auf einen anderen Körper übertragen wird. Dadurch, daß ein Punkt nur einen Teil, nämlich die Ableitung der Gesamtkraft, enthält, wird nicht die Gesamtkraft übertragen sondern nur dessen Ableitung bzw. Modifikation.

4. Die Injektion von Kraft in das System


4.1 Deplazierung von Massen

Massen können auf eine initiale Position gesetzt werden. Das heißt, daß diese Deplazierung einem Energieinput entspricht, der aber nicht von der 0 Position ausgeht. Dies ist mit dem Anzupfen einer Saite vergleichbar, bei der der Finger die Saite deplaziert, um sie dann erst durch das Loslassen frei schwingen zu lassen.

4.2 Versehen einzelner Massen mit einer initialen Kraft


Anders als das Deplazieren einer Masse ist das Versorgen mit einer initialen Kraft eher vergleichbar mit dem Anwerfen eines Pendels, bei dem das Gewicht durch das Anwerfen in Bewegung versetzt wird. Hierbei wird die volle Kraft in das schwingende System injiziert, wobei die Bewegung, im Gegensatz zu der Deplazierten Masse, aus einem Ruhezustand heraus stattfindet.

4.3 Die Anregung von Massen durch komplexe Anregungsstrukturen.


 4.3.1 Conditional Links

Conditional Links simulieren einen Typ von nichtlinearen Links, der in etwas den Beiden Zuständen entspricht, in denen sich 2 Massen berühren, i.e. miteinander fest verbunden sind oder voneinander getrennt sind, wenn sie quasi abgerissen werden. Dabei wird die

4.3.2 Nonlineare Verbindungen zwischen Massen


Neben den linearen Links gibt es auch programmierbare nichtlineare Links. Hierbei wird die Übertragung der Kraft manipuliert und kann somit umgekehrt werden. D.h. kleine Kräfte können sich z.B. als große Kräfte auf die andere Masse übertragen und umgekehrt.

4.3.3 Schwingende Körper als Anregungsstrukturen


Eine andere Möglichkeit Körper in Schwingung zu versetzen kann mit Hilfe komplexer Schwingungsysteme realisiert werden. Dabei werden kleine schwingende Körper, die aus verschiedenen Massen und unterschiedlichen Anregern bestehen gebaut und die resultierende Schwingung, die in ihrer Komplexität schon einem eigenen Klang entspricht, zur Anregung der schwingenden Fläche benutzt.
 

5 Regeln zur Klangerzeugung: 


1. Je größer das schwingende Objekt, desto tiefer der Klang
2. Je schwerer das schwingende Objekt, desto tiefer
3. Je höher der Absorptiongrad, desto kürzer ist der Klang während die hohen Obertöne schneller gedämpft werden.
4. Je höher der die Festigkeit des Materials desto länger ist der Klang, während das Spektrum Obertonreicher ist.

5. Alle Parameter des Klanges können über die Art und Qualität der Kraftinjektion in das System manipuliert werden.

Alle Regeln haben jedoch nicht nur einen einzigen Effekt, sondern ziehen andere Effekte nach sich.

6 Ausblick: 


Der physikalische Klang trägt eine besondere Qualität in sich: er bietet für das Ohr vielfache Bezugspunkte zur Wirklichkeit. Er folgt dabei einer Klanglogik, die sich in dem mechanischen Entstehungsprozeß begründet.
Ästhetisch gesehen liegt hierin sowohl ein Gefahr, als auch ein Potential. Da die Klänge einer bekannten Logik folgen bildet der Hörer zunehmend Referenzen zu existierenden Klangphänomenen und verliert das Klangobjekt selbst aus dem Mittelpunkt der Wahrnehmung. Das Potential phyikalischer Modelle liegt eindeutig in der hohen Qualität und Einfachheit, mit der hier komplexe Spektren und Klangverläufe hergestellt werden können. Ausserdem läßt die Simulation physikalischer Phänomene ein aufwendiges Erforschen und Suchen anderer Klangqualitäten zu das ansonsten schnell an Grenzen unterschiedlichster Art stoßen würde.
Cordis Anima bzw. Genesis stellt hierbei einen Ansatz dar, der sich in seiner Algemeingültigkeit, Einfachheit als sehr aussergewöhnlich darstellt. Die Komplexität des Systems stellt sich auf den Ersten Blick kaum da, aber wer würde schon sagen, dass ein Baustein komplex ist? Komplex werden die Gebilde, die nun mit Hilfe solch generalisierter Methoden von den Komponisten und Forschern realisiert werden können.
 

zu 1. siehe string12b  mit 160 Massen, 12b80, 12b40, 12b20, 12b10.
p /usr/people/ludi/G-WORK/SONS/string/string12b_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b80_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b40_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b20_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b10_defaut.aiff

zu 2. siehe string12b, mit M=1, 12 b1.5 M=1.5, 12l M=2, 12m M=4, 12n M=8, 12o M=16
p /usr/people/ludi/G-WORK/SONS/string/string/string12b_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b1.5_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12l_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12m_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12n_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12o_defaut.aiff

zu 3. siehe string12 z 0.0001, 12b z 0.001, 12c z 0.01, d z 0.1, e z 0.2, f z 0.4
p /usr/people/ludi/G-WORK/SONS/string/string/string12_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12b_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12c_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12d_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12e_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string/string12f_defaut.aiff

zu4. siehe string12g2 k=0.4, 12b k=0.2, 12h k=0.02, i k=0.002, k k=0.0002
p /usr/people/ludi/G-WORK/SONS/string/string12g2_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string12b_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string12h_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string12i_defaut.aiff
p /usr/people/ludi/G-WORK/SONS/string/string12k_defaut.aiff
 

Liste der Klangbeispiele


 
Nr.       Name k          zu 4. z           zu 3. m         zu 2. M      zu 1.
1          12 0.2  0.0001     a 1 160
2          12b 0.2           b 0.001       b 1               a 160          a
3          12b10 0.2 0.001 1 10            b
4          12b20 0.2 0.001 1 20            c
5          12b40 0.2 0.001 1 40            d
6          12b80 0.2 0.001 1 80            e
7          12c 0.2 0.01        c 1 160 
8          12d 0.2 0.1          d 1 160
9          12e 0.2 0.2          e 1 160
10        12f 0.2 0.4          f 1 160
11        12g2 0.4           a 0.001 1 160
12        12h 0.02         c 0.001 1 160
13        12i 0.002       d 0.001 1 160
14        12k 0.0002     e 0.001 1  160
15        12l 0.02 0.001 2               b 160
16        12m 0.02 0.001 4               c 160
17        12n 0.02 0.001 8               d 160
18        12o 0.02 0.001 16             e 160
 

Anregung mit Hilfe nonlinear Links
p quadrat1_defaut.aiff             normaler Gonanschlag
p quadrat11_defaut.aiff           Repititiertes Anschlagen eines Rechtecks als Metallplatte mit LIC
p quadrat16_defaut.aiff           für LIC mit REFs

Anregung mit Conditional Links
a) mit einem Link
p quadrat23_defaut.aiff            Anregung mit komplexer Struktur Ref hat S 0.1
p quadrat23s1_defaut.aiff         wie quadrat23 nur S 1.0
p quadrat23s0_defaut.aiff         wie quadrat23 nur S 0.0
b) mit 6 Links
p quadrat26_defaut.aiff

Anregung mit Deplazierung und Initialkraft
p quadrat1/quadrat23posit_defaut.aiff                Anregung mit einer Initialen Position
p quadrat1/quadrat23vitesmiddle_defaut.aiff     Anregung mit einer Initialkraft an 1 Stelle
p quadrat1/quadrat23vites3point_defaut.aiff      Anregung mit einer Initialkraft an 3 Stellen

Zusammenfassung vier verschiedene Klangmöglichkeiten eines Patches
p quadrat44_defaut.aiff         heller metallerner Klang
p quadrat47_defaut.aiff         dunkle Struktur, wie Mischung aus Metall Holz
p quadrat74_defaut.aiff         als gedämpfte Struktur
p quadrat84_defaut.aiff         als kontinuierliche Struktur