Beschränken wir uns bei digitalen Filtern auf solche, die linear, kausal und zeitinvariant sind, können wir unsere Betrachtungen erheblich vereinfachen. Ein Filter ist
Offensichtlich ist diese Beschränkung musikalisch nicht sehr gravierend. Sie hilft uns aber, da wir somit alle Filter, die wir betrachten wollen mit folgende Formel beschreiben können:
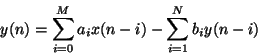
wobei ![]() und
und ![]() Koeffizienten des Filters heißen. Ein solches
Filter hängt von
Koeffizienten des Filters heißen. Ein solches
Filter hängt von ![]() vergangener Eingangswerte, und
vergangener Eingangswerte, und ![]() vergangener
Ausgangswerte ab, die rekursiv weiterverareitet werden.
vergangener
Ausgangswerte ab, die rekursiv weiterverareitet werden.
Ein Filter heißt stabil, wenn der Ausgang, nachdem der Eingang 0 geworden ist, ständig abnimmt, d.h. gegen 0 konvergiert.
Ein Filter, dessen ![]() Koeffizeinten alle 0 sind, ist immer stabil, da es nur von seinem
Eingangssignal abhängt, das ja irgendwann 0 wird. Ein solches Filter
heißt Finite Impulse Response Filter oder FIR-Filter.
Koeffizeinten alle 0 sind, ist immer stabil, da es nur von seinem
Eingangssignal abhängt, das ja irgendwann 0 wird. Ein solches Filter
heißt Finite Impulse Response Filter oder FIR-Filter.
Wird ein Teil des Ausgangssignals wieder in das Filter
zurückgeführt, d.h. ein Teil der ![]() Koeffizeinten ist nicht 0, so
spricht man von rekursiven Filtern. Da der Ausgang eines
rekursiven Filters theoretisch nie 0 wird (sondern sich bestenfalls beliebig
nahe 0 nähert) heißt ein solches Filter Infinite Impulse
Response Filter oder IIR-Filter. Der Ausgang eines solchen
Filters kann eventuell immer größer werden. Solch ein Filter heißt
dann instabil.
Koeffizeinten ist nicht 0, so
spricht man von rekursiven Filtern. Da der Ausgang eines
rekursiven Filters theoretisch nie 0 wird (sondern sich bestenfalls beliebig
nahe 0 nähert) heißt ein solches Filter Infinite Impulse
Response Filter oder IIR-Filter. Der Ausgang eines solchen
Filters kann eventuell immer größer werden. Solch ein Filter heißt
dann instabil.
Die ![]()
![]() Koeffizienten bestimmen (auf durchaus komplizierte Art
und Weise) die Position von
Koeffizienten bestimmen (auf durchaus komplizierte Art
und Weise) die Position von ![]() Nullen oder Antiresonanzen des
Filters, d.h. die Positionen im Spektrum an denen Frequenzen durch das
Filter abgeschwächt werden.
Nullen oder Antiresonanzen des
Filters, d.h. die Positionen im Spektrum an denen Frequenzen durch das
Filter abgeschwächt werden.
Die ![]()
![]() Koeffizienten bestimmen (auf durchaus komplizierte Art
und Weise) die Position von
Koeffizienten bestimmen (auf durchaus komplizierte Art
und Weise) die Position von ![]() Polen oder Resonanzen des
Filters, d.h. die Positionen im Spektrum an denen Frequenzen durch das
Filter angehoben werden. Daher hat ein FIR Filter nur Antiresonanzen,
während ein IIR-Filter mindestens eine Resonanz hat.
Polen oder Resonanzen des
Filters, d.h. die Positionen im Spektrum an denen Frequenzen durch das
Filter angehoben werden. Daher hat ein FIR Filter nur Antiresonanzen,
während ein IIR-Filter mindestens eine Resonanz hat.
Resonanzen und Antiresonanzen können sich gegenseitig bis hin zum völligen Ausgleich beeinflussen. D.h. man kann ein Filter bauen, daß die Frequenzanteile des Eingangssignals unangetastet läßt, also lineare Frequenzrespons hat. Ein soclches Filter kann aber eine durchaus komplexe Phasenrespons haben. Ein solches Filter nennt sich Allpassfilter
FIR Filter können so gestaltet werden, daß sie eine lineare Phasenrespons haben, d.h. es gibt keine Frequenzabhängigen Phasenverschiebungen des Ausgangssignals gegebüber dem Eingangssignal. Der Gebrauch von IIR-Filter hat immer eine gewisse frequenzabhängige Phasenverschiebung zur Folge.